


Next: 2.3 Hartree Fock theory
Up: 2. Electronic structure methods
Previous: 2.1 Introduction
Contents
Subsections
The time independent Schrödinger equation for a system of 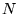 particles interacting via the Coulomb interaction is
particles interacting via the Coulomb interaction is
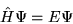 |
(2.1) |
where
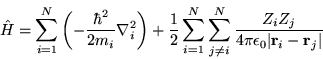 |
(2.2) |
and 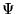 is an N-body wavefunction,
is an N-body wavefunction, 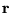 denotes spatial
positions and
denotes spatial
positions and 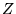 the charges of the individual particles.
the charges of the individual particles. 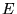 denotes
the energy of either the ground or an excited state of the system.
denotes
the energy of either the ground or an excited state of the system.
Most physical problems of interest consist of a number of interacting
electrons and ions. The total number of particles, 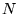 , is usually
sufficiently large that an exact solution cannot be found. Controlled
and well understood approximations are sought to reduce the
complexity to a tractable level. Once the equations are solved, a
large number of properties may be calculated from the wavefunction.
Errors or approximations made in obtaining the wavefunction will be
manifest in any property derived from the wavefunction. Where high
accuracy is required, considerable attention must be paid to the
derivation of the wavefunction and any approximations made.
, is usually
sufficiently large that an exact solution cannot be found. Controlled
and well understood approximations are sought to reduce the
complexity to a tractable level. Once the equations are solved, a
large number of properties may be calculated from the wavefunction.
Errors or approximations made in obtaining the wavefunction will be
manifest in any property derived from the wavefunction. Where high
accuracy is required, considerable attention must be paid to the
derivation of the wavefunction and any approximations made.
A common and very reasonable approximation used in the solution of
equation 2.1 is the Born-Oppenheimer
Approximation. [1] In a system of interacting
electrons and nuclei there will usually be little momentum transfer
between the two types of particles due to their greatly differing
masses. The forces between the particles are of similar magnitude due
to their similar charge. If one then assumes that the momenta of the
particles are also similar, then the nuclei must have much smaller
velocities than the electrons due to their far greater mass. On the
time-scale of nuclear motion, one can therefore consider the electrons
to relax to a ground-state given by the Hamiltonian equation 2.2
with the nuclei at fixed locations. This separation of the electronic
and nuclear degrees of freedom is known as the Born-Oppenheimer
approximation.
This approximation will be used for the remainder of this thesis. It
is important to note that this approximation does not limit the
techniques described to systems of fixed ions: in principle, once the
electronic configuration is known, the nuclear degrees of freedom
could also be solved for, giving rise to nuclear motion.
In practice Newtonian mechanics using forces calculated via quantum
mechanics is often sufficient to solve for the motion of the nuclei,
however, these aspects go beyond the scope of the thesis so that from
now on a simpler version of the many-body Hamiltonian, equation
2.2, is used
The opportunity has been taken to separate the interacting particles
into electrons and ions. The terms in the Hamiltonian are now
expressed in terms of 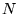 electrons of charge
electrons of charge 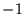 at positions
at positions 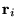 and ions of charge
and ions of charge 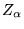 at positions
at positions
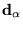 . This simplified electronic Hamiltonian remains very
difficult to solve. No analytic solutions exist for general systems
with more than one electron.
. This simplified electronic Hamiltonian remains very
difficult to solve. No analytic solutions exist for general systems
with more than one electron.
Note that this equation has been written in atomic units
(
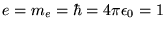 ) which are more convenient for quantum
mechanical problems and will be used for the remainder of the
equations in this thesis.
) which are more convenient for quantum
mechanical problems and will be used for the remainder of the
equations in this thesis.



Next: 2.3 Hartree Fock theory
Up: 2. Electronic structure methods
Previous: 2.1 Introduction
Contents
© Paul Kent
![]() particles interacting via the Coulomb interaction is
particles interacting via the Coulomb interaction is
![]() , is usually
sufficiently large that an exact solution cannot be found. Controlled
and well understood approximations are sought to reduce the
complexity to a tractable level. Once the equations are solved, a
large number of properties may be calculated from the wavefunction.
Errors or approximations made in obtaining the wavefunction will be
manifest in any property derived from the wavefunction. Where high
accuracy is required, considerable attention must be paid to the
derivation of the wavefunction and any approximations made.
, is usually
sufficiently large that an exact solution cannot be found. Controlled
and well understood approximations are sought to reduce the
complexity to a tractable level. Once the equations are solved, a
large number of properties may be calculated from the wavefunction.
Errors or approximations made in obtaining the wavefunction will be
manifest in any property derived from the wavefunction. Where high
accuracy is required, considerable attention must be paid to the
derivation of the wavefunction and any approximations made.
![]() ) which are more convenient for quantum
mechanical problems and will be used for the remainder of the
equations in this thesis.
) which are more convenient for quantum
mechanical problems and will be used for the remainder of the
equations in this thesis.