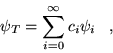 |
(3.11) |
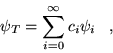 |
(3.11) |
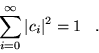 |
(3.12) |
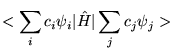 |
|||
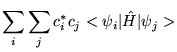 |
|||
| (3.13) |
| (3.14) |
The expectation value of a trial wavefunction with the Hamiltonian must therefore be greater than or equal to the true ground state energy.
Variational calculations depend crucially on the form of trial wavefunction used. By selecting trial wavefunctions on physically motivated grounds, accurate wavefunctions may be obtained. Commonly, wavefunctions obtained from a Hartree-Fock or similar calculations are used and additional parameters added, building-in additional physics such as known limits and derivatives of the many-body wavefunction. The additional variational freedom is then exploited to further optimize the wavefunction. These techniques are briefly described in the remainder of this section, and in more detail in chapters 4 and 5.
Trial wavefunctions, ![]() , are dependent on the set of
, are dependent on the set of ![]() electron positions,
electron positions,
![]() . The expectation value is given by
. The expectation value is given by
| (3.15) |
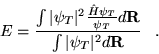 |
(3.16) |
| (3.18) |
The local energy has the useful property that for an exact eigenstate of the Hamiltonian, the local energy is constant. For a general trial wavefunction the local energy is not constant and the variance of the local energy is a measure of how well the trial wavefunction approximates an eigenstate. The spatially averaged variance of the local energy is therefore a quantity suitable for optimisation, and methods exploiting this observation are presented in chapter 5.
Determination of the local energy is one of the most computationally
costly operations performed in QMC calculations. Application of the
Hamiltonian to the trial wavefunction requires computation of the
second derivatives of the wavefunction and the calculation of the
electron-electron and electron-ion potentials. Efficient methods for
the evaluation of
![]() are given in chapter 4.
are given in chapter 4.
Quantum Monte Carlo methods are able to exploit trial wavefunctions of arbitrary forms. Any wavefunction that is physical and for which the value, gradient and laplacian of the wavefunction may be efficiently computed can be used.
The power of Quantum Monte Carlo methods lies in the flexibility of
the form of the trial wavefunction. In early studies of bosonic ![]() He by McMillan [21] the wavefunction was taken
to be a Jastrow or two-body correlation
function, [22]
He by McMillan [21] the wavefunction was taken
to be a Jastrow or two-body correlation
function, [22]
![\begin{displaymath}
\psi=\exp \left[ \sum_{i<j}^{N} -u(r_{ij}) \right] \;\;\;.
\end{displaymath}](pkthimg191.gif) |
(3.19) |
It is important that the trial wavefunction satisfies as many known
properties of the exact wavefunction as possible. A determinantal
wavefunction is correctly anti-symmetric with respect to the exchange
of any two electrons. An additional local set of constraints
which may be readily imposed are for electron-electron and
electron-nucleus coalescence. These constraints are the ``cusp
conditions''[25], and are a constraint on the
derivatives of the wavefunction. For particle-particle coalescence, it
may be shown that [25]
| (3.20) |
A commonly used and simple form of Jastrow factor suitable for solids is
| (3.21) |
| (3.22) |
![\begin{displaymath}
\Psi({\bf R})=D({\bf R}) \exp \left[ \sum_{i<j}^{N}
-u(r_{ij})\right] \;\;\;,
\end{displaymath}](pkthimg202.gif) |
(3.23) |
The development of better approximations to exact many-body wavefunctions, and practical methods for obtaining them will remain an important area of research due to the improved levels of accuracy and efficiency that result. The Jastrow factors used in this thesis contain of the order of 10-200 parameters and details of parameter selection and optimisation are given in the next chapter.
The VMC algorithm consists of two distinct phases. In the first a
walker consisting of an
initially random set of electron positions is propagated according to
the Metropolis algorithm, in order to equilibrate it and begin sampling
![]() . In the second phase, the walker continues to be moved, but
energies and other observables are also accumulated for later averaging and
statistical analysis.
. In the second phase, the walker continues to be moved, but
energies and other observables are also accumulated for later averaging and
statistical analysis.
To simplify the notation,
![]() is used to indicate the
wavefunction with a single electron moved to point
is used to indicate the
wavefunction with a single electron moved to point
![]() and all other electrons unmoved:
and all other electrons unmoved:
In this algorithm, the electrons are moved individually and not as a whole configuration. This improves the efficiency of the algorithm in larger systems, where configuration moves require increasingly small steps to maintain the acceptance ratio. Observables are also accumulated on a per electron basis, weighted by the acceptance and rejection probabilities:
![\begin{displaymath}
<O>=\frac{1}{M}\sum_{i=1}^{M}
\left[p_{i}O_{i}({\bf r}^\prime)+(1-p_{i})O_{i}({\bf r})\right] \;\;\;,
\end{displaymath}](pkthimg209.gif) |
(3.24) |