


Next: 2.6 Summary
Up: 2. Electronic structure methods
Previous: 2.4 Post Hartree-Fock techniques
Contents
Subsections
Density functional theory (DFT) is a powerful, formally
exact theory (see
Refs. [8,9,3] and
references within). It is distinct from quantum chemical methods in
that it is a non-interacting theory and does not yield a correlated 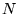 -body
wavefunction. In the Kohn-Sham[10] DFT, the theory is a
one-electron theory and shares many similarities with Hartree-Fock.
DFT has come to prominence over the last decade as a method
potentially capable of very accurate results at low cost. In
practice, approximations are required to implement the theory, and a
significantly variable accuracy results. Calibration studies are
therefore required to establish the likely accuracy in a given class
of systems.
-body
wavefunction. In the Kohn-Sham[10] DFT, the theory is a
one-electron theory and shares many similarities with Hartree-Fock.
DFT has come to prominence over the last decade as a method
potentially capable of very accurate results at low cost. In
practice, approximations are required to implement the theory, and a
significantly variable accuracy results. Calibration studies are
therefore required to establish the likely accuracy in a given class
of systems.
The Hohenberg-Kohn theorem[11] states that if 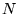 interacting electrons move in an external potential
interacting electrons move in an external potential
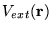 , the ground-state electron density
, the ground-state electron density
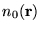 minimises
the functional
minimises
the functional
![\begin{displaymath}
E[n]=F[n]+\int n({\bf r})V_{ext}({\bf r})d{\bf r}
\end{displaymath}](pkthimg73.gif) |
(2.17) |
where 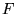 is a universal functional of
is a universal functional of 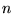 and the minimum value of
the functional
and the minimum value of
the functional 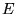 is
is 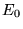 the exact ground-state electronic energy.
the exact ground-state electronic energy.
The proof of equation 2.17 is straightforward. It is a
proof only of existence; additional theory is required before a
method can be implemented.
Levy[12] gave a particularly simple proof of the
Hohenberg-Kohn theorem which is as follows:
A functional 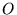 is defined as
is defined as
![\begin{displaymath}
O\left[n({\bf r}) \right]
= \min_{\vert\Psi>\rightarrow n({\bf r})}
\left<\Psi\vert\hat{O}\vert\Psi\right>
\;\;\; ,
\end{displaymath}](pkthimg78.gif) |
(2.18) |
where the expectation value is found by searching over all
wavefunctions, 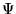 , giving the density
, giving the density 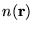 and
selecting the wavefunction which minimises the expectation value of
and
selecting the wavefunction which minimises the expectation value of
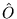 .
.
![$F[n({\bf r})]$](pkthimg81.gif) is defined by
is defined by
![\begin{displaymath}
F\left[n({\bf r}) \right]
= \min_{\vert\Psi>\rightarrow n({\bf r})} \left<\Psi\vert\hat{F}\vert\Psi\right> \;\;\; ,
\end{displaymath}](pkthimg82.gif) |
(2.19) |
so that
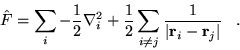 |
(2.20) |
Considering an  -electron ground state wavefunction
-electron ground state wavefunction  which
yields a density
which
yields a density 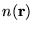 and minimises
and minimises
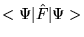 , then from the definition of the functional
, then from the definition of the functional 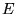
![\begin{displaymath}
E[n({\bf r})] = F[n({\bf r})] + \int n({\bf r})V_{\rm ext}({...
...r})d{\bf r} = <\Psi\vert\hat{F}+V_{\rm ext}\vert\Psi> \;\;\; .
\end{displaymath}](pkthimg86.gif) |
(2.21) |
The Hamiltonian is given by
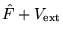 , and so
, and so
![$E[n({\bf r})]$](pkthimg88.gif) must obey the variational principle,
must obey the variational principle,
![\begin{displaymath}
E[n({\bf r})] \geq E_0 \;\;\; .
\end{displaymath}](pkthimg89.gif) |
(2.22) |
This completes the first part of the proof, which places a lower bound
on ![$E[n({\bf r})]$](pkthimg88.gif) .
.
From the definition of ![$F[n({\bf r})]$](pkthimg81.gif) equation 2.19 we obtain
equation 2.19 we obtain
![\begin{displaymath}
F[n_0({\bf r})] \leq <\Psi_0\vert\hat{F}\vert\Psi_0> ,
\end{displaymath}](pkthimg90.gif) |
(2.23) |
since 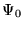 is a trial wavefunction
yielding
is a trial wavefunction
yielding 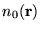 . Combining
. Combining
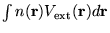 with the above equation gives
with the above equation gives
![\begin{displaymath}
E[n_0({\bf r})] \leq E_0 \;\;\; ,
\end{displaymath}](pkthimg93.gif) |
(2.24) |
which in combination with equation 2.22 yields the key result
![\begin{displaymath}
E[n_0({\bf r})] = E_0 \;\;\; ,
\end{displaymath}](pkthimg94.gif) |
(2.25) |
completing the proof.
Kohn and Sham[10] derived
a coupled set of differential equations enabling the ground state
density 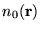 to be found.
to be found.
Kohn and Sham separated ![$F[n({\bf r})]$](pkthimg81.gif) into three distinct parts,
so that the functional
into three distinct parts,
so that the functional 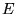 becomes
becomes
![\begin{displaymath}
E\left[n({\bf r}) \right] = T_s\left[n({\bf r}) \right]
+\fr...
...bf r})] + \int n({\bf r})V_{\rm ext}({\bf r})d{\bf r}
\;\;\; ,
\end{displaymath}](pkthimg95.gif) |
(2.26) |
where
![$T_s\left[n({\bf r})\right]$](pkthimg96.gif) is defined as the kinetic energy
of a non-interacting electron gas with density
is defined as the kinetic energy
of a non-interacting electron gas with density 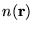 ,
,
![\begin{displaymath}
T_s\left[n({\bf r})\right] = -\frac{1}{2}\sum_{i=1}^N\int
\psi_i^*({\bf r})\nabla^2\psi_i({\bf r})d{\bf r} \;\;\; ,
\end{displaymath}](pkthimg97.gif) |
(2.27) |
and not the kinetic energy of the real
system. Equation 2.26 also defines the exchange-correlation
energy functional ![$E_{XC}[n]$](pkthimg98.gif) . Introducing a normalisation constraint
on the electron density,
. Introducing a normalisation constraint
on the electron density,
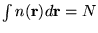 , we obtain
, we obtain
Equation 2.28 may now be rewritten in terms of an effective
potential,
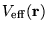 ,
,
![\begin{displaymath}
\frac{\delta T_s\left[n({\bf r})\right]}{\delta n({\bf r})}
+ V_{\rm eff}({\bf r}) = \mu \;\;\; ,
\end{displaymath}](pkthimg105.gif) |
(2.29) |
where
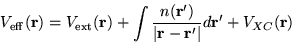 |
(2.30) |
and
![\begin{displaymath}
V_{XC}({\bf r}) = \frac{\delta E_{XC}[n({\bf r})]}{\delta n({\bf r})}
\;\;\; .
\end{displaymath}](pkthimg107.gif) |
(2.31) |
Crucially, non-interacting electrons moving in an
external potential
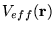 would result in the same
equation 2.29. To find the ground state energy,
would result in the same
equation 2.29. To find the ground state energy, 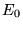 , and
the ground state density,
, and
the ground state density, 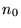 , the one electron Schrödinger
equation
, the one electron Schrödinger
equation
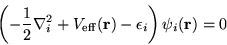 |
(2.32) |
should be solved self-consistently with
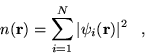 |
(2.33) |
and equations 2.29 and 2.30. A self-consistent
solution is required due to the dependence of
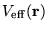 on
on
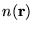 .
.
The above equations provide a theoretically exact method for finding
the ground state energy of an interacting system provided the form of
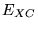 is known. Unfortunately, the form of
is known. Unfortunately, the form of 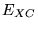 is in general
unknown and its exact value has been calculated for only a
few very simple systems. In electronic structure calculations
is in general
unknown and its exact value has been calculated for only a
few very simple systems. In electronic structure calculations 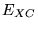 is most commonly approximated within the local density approximation
or generalised-gradient approximation.
is most commonly approximated within the local density approximation
or generalised-gradient approximation.
In the local density approximation (LDA), the value of
![$E_{XC}[n({\bf r})]$](pkthimg115.gif) is approximated by the exchange-correlation
energy of an electron in an homogeneous electron gas of the same
density
is approximated by the exchange-correlation
energy of an electron in an homogeneous electron gas of the same
density 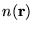 , i.e.
, i.e.
![\begin{displaymath}
E_{XC}^{LDA}[n({\bf r})] = \int
\epsilon_{XC}(n({\bf r}))n({\bf r})d{\bf r} \;\;\; .
\end{displaymath}](pkthimg116.gif) |
(2.34) |
The most accurate data for
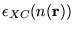 is from Quantum
Monte Carlo calculations.[13]2.3 The LDA is often
surprisingly accurate and for systems with slowly varying charge
densities generally gives very good results. The failings of the LDA
are now well established: it has a tendency to favour more homogeneous
systems and over-binds molecules and solids. In weakly bonded systems
these errors are exaggerated and bond lengths are too short.
In good systems where the LDA works well, often those mostly
consisting of
is from Quantum
Monte Carlo calculations.[13]2.3 The LDA is often
surprisingly accurate and for systems with slowly varying charge
densities generally gives very good results. The failings of the LDA
are now well established: it has a tendency to favour more homogeneous
systems and over-binds molecules and solids. In weakly bonded systems
these errors are exaggerated and bond lengths are too short.
In good systems where the LDA works well, often those mostly
consisting of  bonds, geometries are good and bond lengths and angles
are accurate to within a few percent. Quantities such as the
dielectric and piezoelectric constant are approximately 10% too
large.
bonds, geometries are good and bond lengths and angles
are accurate to within a few percent. Quantities such as the
dielectric and piezoelectric constant are approximately 10% too
large.
The principle advantage of LDA-DFT over methods such as Hartree-Fock
is that where the LDA works well (correlation effects are well
accounted for) many experimentally relevant physical
properties can be determined to a useful level of
accuracy. Difficulties arise where it is not clear whether the LDA is
applicable. For example, although the LDA performs well in bulk
group-IV semiconductors it is not immediately clear how well it
performs at surfaces of these materials.
Despite the remarkable success of the LDA, its limitations mean that
care must be taken in its application. For systems where the density
varies slowly, the LDA tends to perform well, and chemical trends are
well reproduced. In strongly correlated systems where an independent
particle picture breaks down, the LDA is very inaccurate. The
transition metal oxides XO (X=Fe,Mn,Ni) are all Mott insulators, but
the LDA predicts that they are either semiconductors or metals. The
LDA has been applied to high 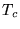 superconductors, but finds
several to be metallic, when in reality they are insulating at
0K. [3]
superconductors, but finds
several to be metallic, when in reality they are insulating at
0K. [3]
The LDA finds the wrong ground state for in many simpler cases. For
example, the LDA finds the wrong ground state for the titanium
atom. The LDA does not account for van der Waals bonding, and gives a
very poor description of hydrogen bonding. These phenomena are essential
for most of biochemistry: the structure of DNA of depends critically
on hydrogen bonding, as do the changes in the structure of most
molecules on solvation.
The success of the LDA has been shown by QMC calculations to result
from a real-space cancellation of errors in the LDA exchange and
correlation energies. [14,15] This is
illustrated in figure 2.1, where the exchange and
correlation energy densities of silicon are compared with an accurate
QMC calculation. The cancellation represents a difficulty when
improvements to the LDA are attempted, as an improvement in only the
exchange or correlation contributions may give worse results.
Figure 2.1:
Contour plots of the LDA exchange and correlation energy
densities compared with VMC calculations for Si in the diamond
structure in the (110) plane: (a)
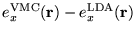 ; (b)
; (b)
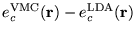 . The chain of atoms and bonds are
represented schematically. The contours are in atomic units. Note
that in the bonding regions between silicon atoms, the error in the
exchange energy density tends to cancel with the error in the
correlation energy density. Figure courtesy
R. Q. Hood. [15]
. The chain of atoms and bonds are
represented schematically. The contours are in atomic units. Note
that in the bonding regions between silicon atoms, the error in the
exchange energy density tends to cancel with the error in the
correlation energy density. Figure courtesy
R. Q. Hood. [15]
|
|
An obvious approach to improving the LDA is to include gradient
corrections, by making 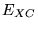 a functional of the density and its gradient:
a functional of the density and its gradient:
![\begin{displaymath}
E_{XC}^{GGA}[n({\bf r})] = \int
\epsilon_{XC}(n({\bf r}))n({...
..._{XC}[n({\bf r}),\vert\nabla n({\bf r})\vert]d{\bf r} \;\;\; ,
\end{displaymath}](pkthimg123.gif) |
(2.35) |
where 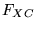 is a correction chosen to satisfy one or several known
limits for
is a correction chosen to satisfy one or several known
limits for 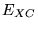 .
.
Clearly, there is no unique recipe for 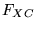 , and several dozen
functionals have been proposed in the literature. They do not always
represent a systematic improvement over the LDA and results must be
carefully compared against experiment.2.4The development of improved functionals is currently a very active
area of research and although incremental improvements are likely, it
is far from clear whether the research will be successful in providing
the substantial increase in accuracy desired.
, and several dozen
functionals have been proposed in the literature. They do not always
represent a systematic improvement over the LDA and results must be
carefully compared against experiment.2.4The development of improved functionals is currently a very active
area of research and although incremental improvements are likely, it
is far from clear whether the research will be successful in providing
the substantial increase in accuracy desired.



Next: 2.6 Summary
Up: 2. Electronic structure methods
Previous: 2.4 Post Hartree-Fock techniques
Contents
© Paul Kent
![]() is defined as
is defined as
![]() is defined by
is defined by
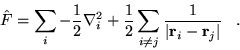
![]() -electron ground state wavefunction
-electron ground state wavefunction ![]() which
yields a density
which
yields a density ![]() and minimises
and minimises
![]() , then from the definition of the functional
, then from the definition of the functional ![]()
![]() equation 2.19 we obtain
equation 2.19 we obtain
![]() into three distinct parts,
so that the functional
into three distinct parts,
so that the functional ![]() becomes
becomes
![\begin{displaymath}
T_s\left[n({\bf r})\right] = -\frac{1}{2}\sum_{i=1}^N\int
\psi_i^*({\bf r})\nabla^2\psi_i({\bf r})d{\bf r} \;\;\; ,
\end{displaymath}](pkthimg97.gif)
![]() ,
,
![]() would result in the same
equation 2.29. To find the ground state energy,
would result in the same
equation 2.29. To find the ground state energy, ![]() , and
the ground state density,
, and
the ground state density, ![]() , the one electron Schrödinger
equation
, the one electron Schrödinger
equation
![]() is known. Unfortunately, the form of
is known. Unfortunately, the form of ![]() is in general
unknown and its exact value has been calculated for only a
few very simple systems. In electronic structure calculations
is in general
unknown and its exact value has been calculated for only a
few very simple systems. In electronic structure calculations ![]() is most commonly approximated within the local density approximation
or generalised-gradient approximation.
is most commonly approximated within the local density approximation
or generalised-gradient approximation.
![\includegraphics [width=15cm]{Figures/si_110_ex_ec.eps}](pkthimg120.gif)
![]() a functional of the density and its gradient:
a functional of the density and its gradient:
![]() , and several dozen
functionals have been proposed in the literature. They do not always
represent a systematic improvement over the LDA and results must be
carefully compared against experiment.2.4The development of improved functionals is currently a very active
area of research and although incremental improvements are likely, it
is far from clear whether the research will be successful in providing
the substantial increase in accuracy desired.
, and several dozen
functionals have been proposed in the literature. They do not always
represent a systematic improvement over the LDA and results must be
carefully compared against experiment.2.4The development of improved functionals is currently a very active
area of research and although incremental improvements are likely, it
is far from clear whether the research will be successful in providing
the substantial increase in accuracy desired.