


Next: 6. Finite-size errors in
Up: 5. Wavefunction optimisation
Previous: 5.9 Other objective functions
Contents
5.10 Conclusions
Several energy and variance minimisation schemes for optimising
many-body wavefunctions were examined, where the integrals involved
are evaluated statistically. Two reasons why variance minimisation
techniques are numerically more stable than energy minimisation
techniques were identified: (i) In variance minimisation it is
allowable to limit the weights or set them equal to unity, which
reduces the variance of the objective function while introducing only
a ``weak bias'', which disappears as the process converges. Altering
the weights in energy minimisation normally leads to a badly behaved
objective function. (ii) Variance minimisation, with or without
altering the weights, shows greater numerical stability against errors
introduced by finite sampling because the positions of the minima of
the variance are not shifted by the finite sampling, whereas those of
the (properly weighted) energy are.
By investigating a model system, configurations with outlying energies
were found to be present and contribute significantly to the variances
of the objective functions. The outlying energies result from
divergences in the kinetic energy in certain, small, regions of
configuration space. Limiting these outlying energies was found to
significantly reduce the variance of variance-like objective
functions, without significantly altering their value.
The best strategy found for optimising wavefunctions based on these
observations is:
- Minimise the variance of the unweighted local energy (objective
function
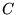 , equation 5.6). This objective function is robust to
finite sampling and has the best statistical properties of the all
objective functions examined.
, equation 5.6). This objective function is robust to
finite sampling and has the best statistical properties of the all
objective functions examined.
- Limit outlying values of the local energy according to
equation 5.15. Limiting the outlying energies greatly reduces the
variance of variance-like objective functions, such as the variance
of the unweighted local energy.
- Regenerate the configurations several times with the updated
parameter values until convergence is obtained. Regeneration of the
configurations reduces the effects of finite sampling, particularly
when the parameters are varied substantially during optimisation.
This strategy may be applied to both ground and excited states of
atoms, molecules and solids. The behaviour observed in numerous
wavefunction optimizations for large systems, presented later in this
thesis, is entirely consistent with the analysis and model system
results presented in this chapter. Although for small systems with
few parameters other methods may be preferable, the above strategy is
expected to be optimal for large systems containing many electrons
where efficiency is critical.
This strategy is applied in the later chapters of this thesis,
particularly in chapter 8 where wavefunctions are
optimised for 13 different carbon clusters. In this application, very
high efficiency was important due to the number (13) and size of the
clusters (up to 128 valence electrons).



Next: 6. Finite-size errors in
Up: 5. Wavefunction optimisation
Previous: 5.9 Other objective functions
Contents
© Paul Kent