| (4.2) |
| (4.2) |
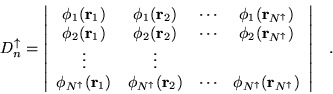 |
(4.3) |
The use
of separate determinants for differing spins results in a trial
function that is not antisymmetric with respect to interchange of
opposite spin electrons, but gives the correct expectation values for
spin-independent operators. [23] The Jastrow
factor, ![]() , in the most general case, is a function of all electron
and atom positions. Jastrow functions are discussed in the next section.
, in the most general case, is a function of all electron
and atom positions. Jastrow functions are discussed in the next section.
The determinantal part of the wavefunction is usually obtained from a
self-consistent method such as LDA-DFT or
HF. [37,38] For most of the calculations
in this thesis a single product of up and down-spin determinants of
orbitals, ![]() , is used to form the wavefunctions. In principle,
configuration-interaction or multi-configuration calculations can be
used to provide multiple determinants, including the coefficients
, is used to form the wavefunctions. In principle,
configuration-interaction or multi-configuration calculations can be
used to provide multiple determinants, including the coefficients
![]() ,4.3 but many applications of QMC have
demonstrated that a high accuracy may usually be obtained using only a single
determinant.
,4.3 but many applications of QMC have
demonstrated that a high accuracy may usually be obtained using only a single
determinant.
The orbitals, ![]() , are expanded in a computationally convenient
basis-set. In principle the orbitals could be expanded in a basis that
is optimal for QMC. The key criterion would be the speed of evaluation
of the value and first and second derivatives of the orbitals at
arbitrary points in space. However, to be obtainable from within a
self-consistent scheme the basis must be convenient for solving the
single-particle equations. Consequently, radial numerical grids,
Gaussian functions [39] and
plane-waves [40] are typically used for atomic,
molecular and continuum systems respectively.4.4
, are expanded in a computationally convenient
basis-set. In principle the orbitals could be expanded in a basis that
is optimal for QMC. The key criterion would be the speed of evaluation
of the value and first and second derivatives of the orbitals at
arbitrary points in space. However, to be obtainable from within a
self-consistent scheme the basis must be convenient for solving the
single-particle equations. Consequently, radial numerical grids,
Gaussian functions [39] and
plane-waves [40] are typically used for atomic,
molecular and continuum systems respectively.4.4
A further consideration is that the orbitals in the Slater determinants must be purely real functions. In supercell (periodic boundary condition) calculations, this is achieved by choosing sets of bloch orbitals such that simple linear combinations of the orbitals yield real functions.
The number of forms of Jastrow factor that have enjoyed repeated use in electronic structure applications is limited. In this section, three forms are presented, two of which are used in subsequent calculations. A thorough study of the efficiency of different forms would be difficult to produce due to the computational cost involved. Alexander and Coldwell [41] reviewed 118 trial wavefunction forms for the He, Li and Be atoms, but did not consider other species, or molecular and continuum systems.
Although the quality of a Jastrow function can be judged by the VMC
energies obtained for candidate systems, compromises must inevitably
be made. Benchmark accuracy Jastrow factors for molecular and
continuum systems typically consist of very large numbers of terms and
parameters. The increase in accuracy per additional term (of a given
kind) inevitably reduces. Consequently, a wavefunction obtaining
![]() of the correlation energy and 30 parameters may be preferable
to one obtaining
of the correlation energy and 30 parameters may be preferable
to one obtaining ![]() of the correlation energy with 200
parameters. For use as a guiding DMC wavefunction, the simpler
wavefunction would be preferable due to the lower computational
cost. For VMC calculations, the preference would depend on the
specific application and desired final accuracy.
of the correlation energy with 200
parameters. For use as a guiding DMC wavefunction, the simpler
wavefunction would be preferable due to the lower computational
cost. For VMC calculations, the preference would depend on the
specific application and desired final accuracy.
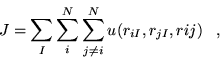 |
(4.4) |
| (4.5) |
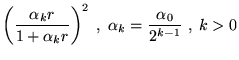 |
(4.6) | ||
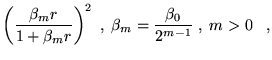 |
(4.7) |
This functional form has yielded wavefunctions of sufficient accuracy to perform DMC calculations in several systems, but has not been systematically tested for accuracy and convergence of VMC energies.
Although successfully used in several calculations, the functional form
has two undesirable features. The correlation function, ![]() , is long
ranged implying that the sum over electrons and ions is not readily
cutoff and will increase in cost with system size. For certain values
of
, is long
ranged implying that the sum over electrons and ions is not readily
cutoff and will increase in cost with system size. For certain values
of ![]() , the long range of the exponential term requires the use
of Ewald summation (section 4.6.1) in supercell
calculations. As this sum involves all pairs of electrons, this
operation would become costly.
, the long range of the exponential term requires the use
of Ewald summation (section 4.6.1) in supercell
calculations. As this sum involves all pairs of electrons, this
operation would become costly.
Additionally, the function is not linear in the ![]() parameters,
which is desirable to avoid full recalculation of the function as the
parameters are changed during optimisation. This increases the
computational cost of the optimisation (see section 4.7.1).
parameters,
which is desirable to avoid full recalculation of the function as the
parameters are changed during optimisation. This increases the
computational cost of the optimisation (see section 4.7.1).
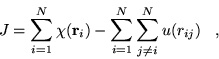 |
(4.8) |
The electron-electron dependent part of the Jastrow function consists
of cusp-satisfying part and a separate power expansion, both of which
are constrained to be short ranged. For the cusp-satisfying part, the
following form was chosen:
The parameters ![]() ,
, ![]() are different for spin parallel and
anti-parallel electron pairs, to model the additional Pauli repulsion
experienced by parallel spin electrons. These functions satisfy the
electron-electron cusp condition and are continuous in value and first
derivative. The expansion range,
are different for spin parallel and
anti-parallel electron pairs, to model the additional Pauli repulsion
experienced by parallel spin electrons. These functions satisfy the
electron-electron cusp condition and are continuous in value and first
derivative. The expansion range, ![]() , is chosen to be less than or
equal to the Wigner-Seitz radius in supercell calculations avoiding
the need to perform an Ewald sum. A further advantage of the Chebyshev
expansion is that unlike the terms in a simple power expansion, the
terms carry equal weight over their range and consequently exhibit
greater stability during optimisation.
, is chosen to be less than or
equal to the Wigner-Seitz radius in supercell calculations avoiding
the need to perform an Ewald sum. A further advantage of the Chebyshev
expansion is that unlike the terms in a simple power expansion, the
terms carry equal weight over their range and consequently exhibit
greater stability during optimisation.
In applications to bulk carbon and silicon, wavefunctions obtaining
![]() of the fixed-node DMC correlation energy were obtained. The
high accuracy of these wavefunctions indicates that the limited
range (form) of the correlation functions does not severely limit the
accuracies obtained.
of the fixed-node DMC correlation energy were obtained. The
high accuracy of these wavefunctions indicates that the limited
range (form) of the correlation functions does not severely limit the
accuracies obtained.
A general power expansion, in ![]() and
and ![]() , about an atom over a
range
, about an atom over a
range ![]() must satisfy similar conditions to Williamson's function,
above: the function must go to zero at
must satisfy similar conditions to Williamson's function,
above: the function must go to zero at ![]() and be continuous in value
and first derivative. The atom centred power expansion in electron-ion
distance,
and be continuous in value
and first derivative. The atom centred power expansion in electron-ion
distance, ![]() and electron-electron distance
and electron-electron distance ![]() contains 5
independent series: [48,49]
contains 5
independent series: [48,49]
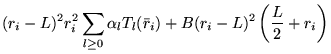 |
(4.13) | ||
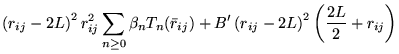 |
|||
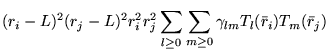 |
|||
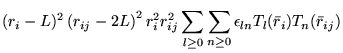 |
|||
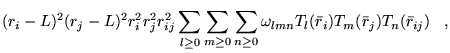 |
| (4.14) |
The overall Jastrow factor consists of sets of the above functions
supplemented by the electron-electron cusp-satisfying ![]() term,
equation 4.10, and the homogeneous
term,
equation 4.10, and the homogeneous ![]() -dependent
-dependent ![]() term, equation 4.11. This is shown schematically in
figure 4.1.
term, equation 4.11. This is shown schematically in
figure 4.1.
![\includegraphics [width=10cm]{Figures/acjast.eps}](pkthimg339.gif)
|
For the main applications in this thesis, only the terms ![]() were
used as sufficient accuracy was obtained and the full series had yet
to be implemented. In tests on the ground state of an all-electron
oxygen atom, using exact HF orbitals,
were
used as sufficient accuracy was obtained and the full series had yet
to be implemented. In tests on the ground state of an all-electron
oxygen atom, using exact HF orbitals, ![]() of the experimental
correlation energy was obtained using all the terms, approximately
of the experimental
correlation energy was obtained using all the terms, approximately
![]() more than a wavefunction using only the
more than a wavefunction using only the ![]() terms. This
accuracy is similar to that obtained in pseudopotential
calculations of oxygen atoms, demonstrating the importance of the
additional correlation terms when treating core electrons.
terms. This
accuracy is similar to that obtained in pseudopotential
calculations of oxygen atoms, demonstrating the importance of the
additional correlation terms when treating core electrons.