- ... found2.1
- The
solution found for the orbitals will be the ``best fit'' solution in a least-squares
sense.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
wavefunctions.2.2
- Methods to apply perturbative corrections to
configuration interaction have been developed. Applying perturbative
corrections to a configuration interaction-derived wavefunction can
be an efficient way of improving accuracy at lower cost than
performing a higher level configuration interaction-based
calculation. Uses of these techniques are quite specialised and give a
small non-variational correction to the CI energy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...DMCeperleyPRL19802.3
- Published
in 1980, this is now one of the oldest, most widely referenced papers
in the field of numerical electronic structure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... experiment.2.4
- An illustration of
this point is found in chapter 8, where different
functionals give significantly different energetic orderings compared
with QMC calculations for carbon clusters up to
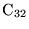 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
presented.4.1
- This topic is studied further in
chapter 5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... calculations,4.2
- Even within DFT and quantum
chemical methods, the use of pseudopotentials is often
unavoidable. Pseudopotentials allow the use of far smoother
wavefunctions, greatly reducing the number of basis functions
required. In the case of a plane-wave basis, most commonly employed
in solid-state calculations, the use of pseudopotentials is almost
essential. A hidden pseudopotential-like approximation is frequently
made in quantum chemical calculations: that of neglecting selected
core molecular orbitals from correlation calculations. This
``frozen-core'' approximation is almost essential for large-scale
quantum chemical calculations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,4.3
- Multiple determinants are particularly effective in
systems with small gaps. For large gap systems, multiple determinants
provide only a small (inefficient) improvement in the wavefunction. In
the Be atom, a trial function consisting of
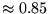 of the
of the
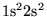 ground state and
ground state and 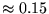 of the low
lying
of the low
lying
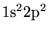 excited states and optimised Jastrow
factor is found to obtain significantly more correlation energy
(
excited states and optimised Jastrow
factor is found to obtain significantly more correlation energy
(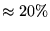 ) than a wavefunction consisting of the ground state
determinant and an optimised Jastrow factor. In
chapter 8, a 43 determinant wavefunction is used for a
) than a wavefunction consisting of the ground state
determinant and an optimised Jastrow factor. In
chapter 8, a 43 determinant wavefunction is used for a
 ring.
ring.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectively.4.4
- Due to basis
set incompleteness, a subsequent projection onto a basis more suited
to QMC applications is numerically treacherous. However, as we are
only dealing with trial wavefunctions, this approach remains a
potential area of future research.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time.4.5
- The proportion of
time spent is very case-dependent, but proportions between
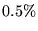 and
and 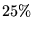 were observed during the calculations in this thesis.
were observed during the calculations in this thesis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
directly.4.6
- In pseudopotential calculations,
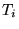 and
and
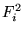 were found to have worse statistics than the kinetic
energy. However, in all-electron VMC calculations of the oxygen atom and
water monomer using
exact and near-exact HF orbitals respectively, the kinetic energy was
found to have worse statistical errors by a factor of approximately 2. No
mention of this was found in the literature.
were found to have worse statistics than the kinetic
energy. However, in all-electron VMC calculations of the oxygen atom and
water monomer using
exact and near-exact HF orbitals respectively, the kinetic energy was
found to have worse statistical errors by a factor of approximately 2. No
mention of this was found in the literature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
atoms,4.7
- Arguably, sufficiently accurate wavefunctions may be
constructed for all first row
elements. Ref.[53] includes wavefunctions for
first-row dimers obtaining
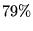 or greater of the experimentally
determined correlation energy.
or greater of the experimentally
determined correlation energy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... accuracy.4.8
- In
general, atoms with a large energetic separation of core and valence
levels have cores that can be accurately represented by a
pseudopotential. This is not always the case however: some third row
elements maintain good core-valence separation, but in certain
materials, such as Ga compounds, the occupied
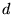 -levels are found to
significantly influence bonding. In these cases, additional electrons
must be placed in the valence and a smaller core used.
-levels are found to
significantly influence bonding. In these cases, additional electrons
must be placed in the valence and a smaller core used.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cell.6.1
- The
reduction of the problem to one within the primitive unit cell is only
possible within independent particle theories; in a true many-body
theory one has to solve over the entire simulation cell.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... shown.6.2
- These results are similar
to those given in Ref. [87], but they have been
fully recalculated and corrected.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
``cumulenic''8.1
- Have only identical bond lengths.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ``polyacetylenic''8.2
- Have alternating bond lengths.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.