


Next: 3.3 Variational Monte Carlo
Up: 3. Quantum Monte Carlo
Previous: 3.1 Introduction
Contents
Subsections
Monte Carlo methods were first developed as a method for estimating
integrals that could not be evaluated analytically. Although many
statistical techniques are now included in the category of ``Monte
Carlo methods''[16,17], the method
used in this thesis is principally Monte Carlo integration.
A straightforward application of Monte Carlo is the evaluation of
definite integrals. Consider the one dimensional integral
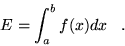 |
(3.1) |
By application of the mean value theorem of calculus, the integral may
be approximated by
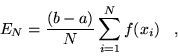 |
(3.2) |
where the points 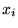 fully cover the range of integration. In the
limit of a large number of points
fully cover the range of integration. In the
limit of a large number of points 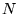 ,
, 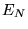 tends to the exact value
tends to the exact value
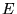 .
.
A conventional choice for the points 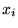 would be a uniform
grid. More accurate methods of numeric quadrature, such as Simpson's
rule and Gaussian quadrature[18]
use a weighted average of the points:
would be a uniform
grid. More accurate methods of numeric quadrature, such as Simpson's
rule and Gaussian quadrature[18]
use a weighted average of the points:
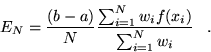 |
(3.3) |
These methods are highly effective for low dimensional integrals. The
computational cost of evaluating an integral, to a fixed accuracy, of
dimensionality 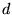 increases as
increases as 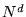 . An alternate and more efficient
approach is to select the points
. An alternate and more efficient
approach is to select the points 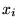 randomly, from a given
probability distribution by Monte Carlo methods.
randomly, from a given
probability distribution by Monte Carlo methods.
If points are selected at random over the interval ![$[a,b]$](pkthimg133.gif) , the Monte
Carlo estimate of the integral, equation
, the Monte
Carlo estimate of the integral, equation
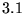 , becomes
, becomes
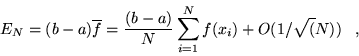 |
(3.4) |
where 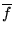 denotes the mean value of
denotes the mean value of 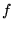 over the set of
sampled points
over the set of
sampled points 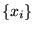 . By the central limit
theorem, [19] the set of all possible sums over
different
. By the central limit
theorem, [19] the set of all possible sums over
different 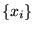 will have a Gaussian distribution. The standard
deviation
will have a Gaussian distribution. The standard
deviation 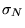 of the different values of
of the different values of 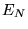 is a measure of
the uncertainty in the integral's value
is a measure of
the uncertainty in the integral's value
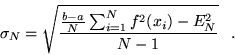 |
(3.5) |
The probability that 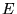 is within
is within
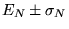 is
is 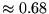 and the probability of being with
and the probability of being with 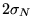 is
is 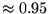 . This
error decays as
. This
error decays as 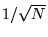 independent of the dimensionality
of the integral, unlike grid based methods which have a strong
dimensional dependence.
independent of the dimensionality
of the integral, unlike grid based methods which have a strong
dimensional dependence.
Simple schemes for Monte Carlo integration can suffer from low
efficiency. Many functions of interest have significant weight in only
a few regions. For example, most of the contributions to an integral
of a simple Gaussian are located near the central peak. In a simple
Monte Carlo integration scheme, points are sampled uniformly, wasting
considerable effort sampling the tails of the Gaussian. Techniques for
overcoming this problem act to increase the density of points in
regions of interest and hence improve the overall efficiency. These
techniques are called importance sampling.
Points are sampled from a non-uniform
distribution 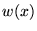 , where
, where 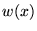 is always positive and chosen to
approximate
is always positive and chosen to
approximate 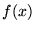 over the region of interest. The integral may now
be evaluated by selecting points from the probability distribution
over the region of interest. The integral may now
be evaluated by selecting points from the probability distribution
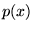 ,
,
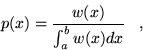 |
(3.6) |
so that the integral may be evaluated
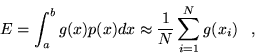 |
(3.7) |
where
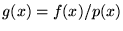 and the points
and the points 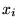 are generated from the
probability distribution
are generated from the
probability distribution 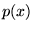 .
.
Provided 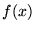 is well described by
is well described by 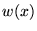 ,
, 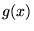 remains close to
unity, so that the standard deviation defined in equation
3.5 is greatly reduced. (The best possible choice
for
remains close to
unity, so that the standard deviation defined in equation
3.5 is greatly reduced. (The best possible choice
for 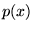 is
is 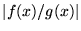 .) The integration procedure is therefore more
efficient, although the error still decays as
.) The integration procedure is therefore more
efficient, although the error still decays as 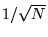 .
.
In this thesis, the Metropolis algorithm[20] is
used in the importance sampling of multi-dimensional integrals. The
Metropolis algorithm generates a random walk of points
distributed according to a required probability distribution. From an
initial ``position'' in phase or configuration space, a proposed ``move''
is generated and the move either accepted or rejected according to the
Metropolis algorithm. By taking a sufficient number of trial steps all
of phase space is explored and the Metropolis algorithm ensures that
the points are distributed according to the required probability
distribution.
The Metropolis algorithm may be derived by considering the
probability density, 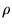 at two points in configuration space
at two points in configuration space 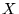 and
and
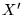 . Configuration space is specified by the integration
variables and limits. For one dimensional integration,
. Configuration space is specified by the integration
variables and limits. For one dimensional integration, 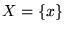 for
for
![$x \in [a,b]$](pkthimg158.gif) . Averaged over many trial steps, the
average number of samples at
. Averaged over many trial steps, the
average number of samples at 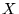 and
and 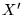 should be equal,
should be equal,
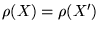 .
.
The probability for a trial move from 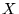 to
to 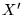 defined
defined
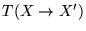 and we require
and we require
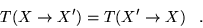 |
(3.8) |
If the probability of accepting a move from 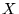 to
to 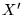 is
is
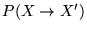 then the total probability of accepting a
move from
then the total probability of accepting a
move from 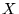 to
to 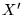 is
is
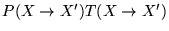 . Therefore, at equilibrium
. Therefore, at equilibrium
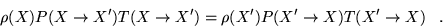 |
(3.9) |
The Metropolis algorithm corresponds to choosing
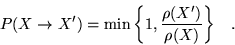 |
(3.10) |
For the Metropolis algorithm to be valid, it is essential that the
random walk is ergodic, that is any point 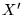 in configuration
space may be reached from any other point
in configuration
space may be reached from any other point 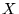 . In some applications of
the Metropolis algorithm, parts of configuration space may be
difficult to reach. Long simulations or a modification of the
algorithm are then necessary. Many methods have been developed to cope
with this ``slowing down'', [16] but for the
applications presented here the Metropolis algorithm has been found
both adequate and sufficient for the problems investigated.
. In some applications of
the Metropolis algorithm, parts of configuration space may be
difficult to reach. Long simulations or a modification of the
algorithm are then necessary. Many methods have been developed to cope
with this ``slowing down'', [16] but for the
applications presented here the Metropolis algorithm has been found
both adequate and sufficient for the problems investigated.



Next: 3.3 Variational Monte Carlo
Up: 3. Quantum Monte Carlo
Previous: 3.1 Introduction
Contents
© Paul Kent
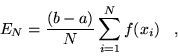
![]() would be a uniform
grid. More accurate methods of numeric quadrature, such as Simpson's
rule and Gaussian quadrature[18]
use a weighted average of the points:
would be a uniform
grid. More accurate methods of numeric quadrature, such as Simpson's
rule and Gaussian quadrature[18]
use a weighted average of the points:
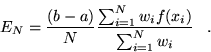
![]() , the Monte
Carlo estimate of the integral, equation
, the Monte
Carlo estimate of the integral, equation
![]() , becomes
, becomes
![]() , where
, where ![]() is always positive and chosen to
approximate
is always positive and chosen to
approximate ![]() over the region of interest. The integral may now
be evaluated by selecting points from the probability distribution
over the region of interest. The integral may now
be evaluated by selecting points from the probability distribution
![]() ,
,
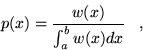
![]() is well described by
is well described by ![]() ,
, ![]() remains close to
unity, so that the standard deviation defined in equation
3.5 is greatly reduced. (The best possible choice
for
remains close to
unity, so that the standard deviation defined in equation
3.5 is greatly reduced. (The best possible choice
for ![]() is
is ![]() .) The integration procedure is therefore more
efficient, although the error still decays as
.) The integration procedure is therefore more
efficient, although the error still decays as ![]() .
.
![]() at two points in configuration space
at two points in configuration space ![]() and
and
![]() . Configuration space is specified by the integration
variables and limits. For one dimensional integration,
. Configuration space is specified by the integration
variables and limits. For one dimensional integration, ![]() for
for
![]() . Averaged over many trial steps, the
average number of samples at
. Averaged over many trial steps, the
average number of samples at ![]() and
and ![]() should be equal,
should be equal,
![]() .
.
![]() to
to ![]() defined
defined
![]() and we require
and we require
![]() in configuration
space may be reached from any other point
in configuration
space may be reached from any other point ![]() . In some applications of
the Metropolis algorithm, parts of configuration space may be
difficult to reach. Long simulations or a modification of the
algorithm are then necessary. Many methods have been developed to cope
with this ``slowing down'', [16] but for the
applications presented here the Metropolis algorithm has been found
both adequate and sufficient for the problems investigated.
. In some applications of
the Metropolis algorithm, parts of configuration space may be
difficult to reach. Long simulations or a modification of the
algorithm are then necessary. Many methods have been developed to cope
with this ``slowing down'', [16] but for the
applications presented here the Metropolis algorithm has been found
both adequate and sufficient for the problems investigated.