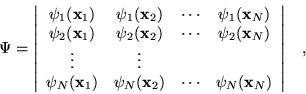2.3 Hartree Fock theory

Hartree Fock theory is one the simplest approximate theories for solving the many-body Hamiltonian. It is based on a simple approximation to the true many-body wavefunction: that the wavefunction is given by a single Slater determinant of $N$ spin-orbitals

$$\Psi = \left\vert \begin{array}{cccc} \psi_1({\bf x}_1) & \... ...\cdots & \psi_N({\bf x}_N)\\ \end{array} \right\vert 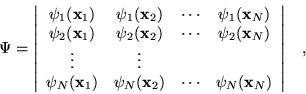\;\;\; ,$$ (2.4)

where the variables ${\bf x}$ include the coordinates of space and spin. This simple ansatz for the wavefunction $\Psi$ captures much of the physics required for accurate solutions of the Hamiltonian. Most importantly, the wavefunction is antisymmetric with respect to an interchange of any two electron positions. This property is required by the Pauli exclusion principle, i.e.

$$\Psi({\bf x}_1,{\bf x}_2,\ldots,{\bf x}_i,\ldots,{\bf x}_j,\... ...2,\ldots,{\bf x}_j,\ldots,{\bf x}_i,\ldots,{\bf x}_N) \;\;\; .$$ (2.5)

This wavefunction may be inserted into the Hamiltonian, equation 2.3, and an expression for the total energy derived. [2,3,4] Applying the theorem that the value of a determinant is unchanged by any non-singular linear transformation, we may choose the $\psi$ to be an orthonormal set. We now introduce a Lagrange multiplier $\epsilon_{i}$ to impose the condition that the $\psi$ are normalised, and minimise with respect to the $\psi$

$$\frac{\delta}{\delta\psi}\left[<\hat{H}>-\sum_j\epsilon_j\int\vert\psi_j\vert^2d{\bf r}\right] = 0 \;\;.$$ (2.6)

An enormous simplification of the expressions for the orbitals $\psi$ results. They reduce to a set of one-electron equations of the form

$$-\frac{1}{2}\nabla^2\psi_i({\bf r})+V_{ion}({\bf r})\psi_i({... ...bf r})\psi_i({\bf r}) = \epsilon_{i} \psi_{i}({\bf r}) \;\;\;,$$ (2.7)

where $U({\bf r})$ is a non-local potential and the local ionic potential is denoted by $V_{ion}$. The one-electron equations resemble single-particle Schrödinger equations.

The full Hartree-Fock equations are given by

$$\epsilon_i\psi_i({\bf r}) = \left(-\frac{1}{2}\nabla^2+V_{ion}({\bf r}) \right)\psi_i({\bf r}... ...'\frac{\vert\psi_j({\bf r}')\vert^2}{\vert{\bf r}-{\bf r}'\vert}\psi_i({\bf r})$$

$$- \sum_j \delta_{\sigma_i \sigma_j}\int d{\bf r}'\frac{\psi_j^*({\bf r}')\psi_i({\bf r}')}{\vert{\bf r}-{\bf r}'\vert}\psi_j({\bf r}) \;\;\;.$$ (2.8)

The right hand side of the equations consists of four terms. The first and second give rise are the kinetic energy contribution and the electron-ion potential. The third term, or Hartree term, is the simply electrostatic potential arising from the charge distribution of $N$ electrons. As written, the term includes an unphysical self-interaction of electrons when $j=i$. This term is cancelled in the fourth, or exchange term. The exchange term results from our inclusion of the Pauli principle and the assumed determinantal form of the wavefunction. The effect of exchange is for electrons of like-spin to avoid each other. Each electron of a given spin is consequently surrounded by an ``exchange hole'', a small volume around the electron which like-spin electron avoid.

The Hartree-Fock approximation corresponds to the conventional single-electron picture of electronic structure: the distribution of the $N$ electrons is given simply by the sum of one-electron distributions $\vert\psi\vert^2$. This allows concepts such as labelling of electrons by angular momenta (`` a 3d electron in a transition metal''), but it must be remembered that this is an artifact of the initial ansatz and that in some systems modifications are required to these ideas.

Hartree-Fock theory, by assuming a single-determinant form for the wavefunction, neglects correlation between electrons. The electrons are subject to an average non-local potential arising from the other electrons, which can lead to a poor description of the electronic structure. Although qualitatively correct in many materials and compounds, Hartree-Fock theory is insufficiently accurate to make accurate quantitative predictions.

2.3.0.1 Basis set expansion

In the preceding section, the single-particle Hartree-Fock equations were presented (equation 2.8). Numerical solutions usually are found by expanding the orbitals in a basis set.

$$\psi_{i}=\sum_{k}^{M} c_{ik} \phi_{k}$$ (2.9)

The unknown Hartree-Fock orbitals, $\psi$, are written as a linear expansion in $M$ known basis functions $\phi$. Inserting equation 2.9 into equation (2.8) leads to a set of matrix equations for the expansion coefficients, $c_{ik}$. The problem of solving the Hartree-Fock equations is reduced to a linear algebra problem, which may be solved by techniques such as iterative diagonalisation. [5,6]

In practice, a basis of plane waves in periodic systems or localised Gaussians in finite systems, is commonly used. The basis set expansion represents an additional limitation of the techniques: unless the basis set expansion has sufficient freedom to encompass the exact solutions for the Hartree-Fock orbitals, $\phi$, a compromise solution with a higher Hartree-Fock energy will be found^2.1. In practical applications, convergence of the basis set must be studied to verify that the expansion is sufficiently complete.