5.7 Tests of minimisation procedures

It is important that any theoretical improvements in minimisation procedures are tested in actual calculations. In order to test the different procedures at an affordable computational cost, a non-interacting test system was selected. In a non-interacting system the exact wavefunction for the system is known, which helps in the analysis of minimisation procedures. We believe that the conclusions drawn from this systems are general because in more realistic calculations the problems simply become more serious.

5.7.1 The model system

A non-interacting model of the valence states of silicon in the diamond structure was chosen, using periodic boundary conditions to simulate the solid. This system is representative of the systems considered in current calculations, provided any instabilities in actual optimisations are not due to electron-electron interactions.

The model system consistent of an fcc simulation cell containing 16 atoms and 64-electrons. The electrons were subject to a local potential which is described by two Fourier components, $V_{111}$ = -0.1 a.u., and $V_{220}$ = -0.06 a.u., chosen to give a reasonable description of the valence bandstructure of silicon. These values are in reasonable agreement with empirical pseudopotential form factors for silicon [85]. Overall this model gives a reasonable description of the valence states of silicon and retains the essential features for testing the optimization techniques.

Near exact single-particle orbitals were obtained by diagonalising the Hamiltonian in a plane-wave basis set containing all waves up to a kinetic energy cutoff of 15 a.u. This basis set is still incomplete, but the square root of the variance of the energy is about 0.02 eV per atom, which is negligible for current purposes. A variational parameter, $\alpha$, was added to the wavefunction in the form of a $\chi$ function with the full symmetry of the diamond structure:

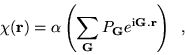$$\chi ({\bf r})=\alpha\left( \mathop{\displaystyle \sum } \limits_{{\bf G}}P_{{\bf G}}e^{{\rm i}{\bf G.r}}\right) \;\;,$$ (5.10)

where ${\bf G}$ labels the 8 reciprocal lattice vectors of the [111] star and $P_{{\bf G}}$ is a phase factor associated with the non-symmorphic symmetry operations. The many-body wavefunction is given by

$$\psi=D^{\uparrow}D^{\downarrow} \exp\left[ \sum_{i=1}^{N} \chi({\bf r}_{i})\right] \;\;\;.$$ (5.11)

The exact value of the parameter, $\alpha$, is, of course, zero. To model the situation where the wavefunction does not possess the variational freedom to encompass the exact one we used a smaller basis set cutoff of 2.5 a.u. The variational energy from this wavefunction is 0.35 eV per atom above the exact value, which is typical of the values we encounter in our solid state calculations. The optimal value of $\alpha$ for this inexact wavefunction is very close to zero.

This model exhibits all the numerical problems encountered in optimization procedures. In practical situations one may have more electrons and more parameters to optimize, which makes the numerical instabilities more pronounced. In order to analyse the behaviour in detail the variance of the difference objective functions was analysed. Unfeasibly large numbers of electron configurations were required to obtain accurate values of the variance of the objective functions for wavefunctions with more electrons and variable parameters than used in the model system. For these systems, improvements in optimisation procedures will be even more advantageous.

5.7.2 Generation of test ensemble

A sample of $0.96\times 10^{6}$ statistically independent electronic configurations was generated and used to calculate the quantities involved in the various optimization schemes. In practical QMC applications, a typical number of configurations used for optimisation might be $10^4$, but it was necessary to use a much larger number in these tests to obtain sufficiently accurate values of the different objective functions and, in particular, their variances. In a practical application an objective function, say $C(\alpha)$, is evaluated using, say, $10^4$ configurations. The quantities of interest are then $C(\alpha)$ and its variance calculated as averages over blocks of $10^4$ configurations.

The configurations were generated by a Metropolis walk distributed according to $\Phi^2$, using the (inexact) reduced basis-set wave function. An optimization procedure typically starts with non-optimal parameter values which are improved during the optimization procedure. Results are presented for configurations generated with the non-optimal value of $\alpha_0$ = 0.03, which gives results typical of the starting value for an optimization, and $\alpha_0$ = 0, which is the final value from a successful optimization procedure. The qualitative behaviour was found to be not strongly influenced by the value of $\alpha_0$.

5.7.3 Results

Energy minimisation schemes are considered first. In figure 5.1 the weighted and unweighted mean energies, $E_{\rm V}$ and $E_C$, and their variances as a function of $\alpha$ are shown, with configurations generated from $\alpha_0$ = 0.03 (figure 5.1a) and $\alpha_0$ = 0 (figure 5.1b).

The unweighted mean energy has a maximum at $\alpha_0$, i.e., the value from which the configurations were generated. This result can be understood as follows. Consider a wave function of the form

$$\Phi = D^{\uparrow}D^{\downarrow} \exp \left[\sum_k \alpha_k J_k \right] \;\;,$$ (5.12)

where the $\alpha_k$ are parameters, the $J_k$ are correlation functions and the $D^{\uparrow}$, $D^{\downarrow}$ are up and down-spin determinants. The mean unweighted energy (equation 5.7) can be written as

$$E_{C}(\{\alpha_k\}) = (\alpha_k - \alpha_{k0})\,G_{kl}\,(\alpha_l - \alpha_{l0})\;\;+\;\;{\rm constant}\;\;,$$ (5.13)

where $\alpha_{k0}$ are the parameter values from which the configurations are generated and

$$G_{kl} = \frac{-\frac{1}{2} \int \Phi^2(\{\alpha_{k0}\}) \su... ..._l \, d{\bf R}}{\int \Phi^2(\{\alpha_{k0}\}) \, d{\bf R}}\;\;.$$ (5.14)

The $G_{kl}$ and the constant term depend on the $\alpha_{k0}$ but not on the $\alpha_k$. When there is only a single parameter, $G$ is negative, so that $E_C$ is a quadratic function with a maximum at $\alpha_k = \alpha_{k0}$. When there is more than one parameter the stationary point of the quadratic can be a maximum, minimum or saddle point, which is not acceptable behaviour for an objective function. The weights may be altered in other ways, such as limiting their upper value, but if the weights are altered the minima of the energy are moved, which is a ``strong bias'' in the objective function. Therefore, if an energy minimisation method is used, weights must be included.

Figure 5.1: Weighted and unweighted mean energies and standard deviations, shown as error bars, for configurations generated with (a) $\alpha_0$=0.03 and (b) $\alpha_0$=0.

The distributions of the weights and local energies of the test ensemble are now examined. In figure 5.2 the distributions of the weights for $\alpha_0$ = 0.03 and $\alpha$ = 0 and for $\alpha_0$ = 0 and $\alpha$ = 0.03 are plotted, while in figure 5.3 the corresponding distributions of the local energies are shown. The distributions of the weights resemble Poisson distributions, but the square roots of the variances are significantly greater than the means, so there are more configurations at large weights than for a Poisson distribution with the same mean. The local energies follow normal distributions relatively well. As expected, the distributions of the local energies is wider for the $\alpha_0$ = 0.03 wavefunction. Closer inspection reveals that the distribution of the local energies is not exactly normal because the actual distributions have ``fat tails''. The outlying energies result from outlying values of the kinetic energy. The standard deviations are $\sigma$ = 0.964 a.u. and $\sigma$ = 0.726 a.u., for $\alpha_0$ = 0.03 and 0, respectively. The expected percentage of configurations beyond 3$\sigma$ from the mean of a normal distribution is 0.27%, but the actual percentages are 0.443% and 0.608% for $\alpha_0$ = 0.03 and 0, respectively. Although these outlying local energies give a negligible contribution to the mean energy, calculated with or without weighting, and only a very small contribution to the values of the variance-like objective functions, $A(\alpha)$, $B(\alpha)$, and $C(\alpha)$, they give significant contributions to the variances of the variance-like objective functions.

Figure 5.2: Distributions of weights for configurations generated with $\alpha_0$=0.03 and $\alpha_0$=0, evaluated with $\alpha$=0 and $\alpha$=0.03, respectively.

Figure 5.3: Distributions of the local energies for $\alpha$=0 and $\alpha$=0.03.