The calculation of excited state energies in solids using QMC methods is a fairly new area of research. The method described here obtains a large number of excitation energies from a single QMC calculation involving averages over the ground state wave function.
The Extended Koopmans' Theorem (EKT) was derived apparently
independently by Smith, Day and Garrod[98] and by
Morrell, Parr and Levy.[99] The EKT is closely
related to the earlier work of Feynman[131] on
calculating excitation energies in the superfluid state of He![]() ,
although the quantum chemists appear to have developed the theory
independently. The EKT has been shown to give very good excitation
energies for simple molecular systems,[132] and has
been applied to atomic and diatomic
systems.[133,134] It appears
particularly well suited to QMC calculations in which explicitly
correlated many-body wave functions are used. The
derivation is reviewed following Ref. [98], and a
variation suitable for QMC is formulated.
,
although the quantum chemists appear to have developed the theory
independently. The EKT has been shown to give very good excitation
energies for simple molecular systems,[132] and has
been applied to atomic and diatomic
systems.[133,134] It appears
particularly well suited to QMC calculations in which explicitly
correlated many-body wave functions are used. The
derivation is reviewed following Ref. [98], and a
variation suitable for QMC is formulated.
In this method the band energies are calculated as ionisation
energies. The starting point is an approximation to the normalized ground
state wave function, ![]() . The wave function for the
. The wave function for the ![]() -1
electron system is approximated by the Ansatz of eliminating an
orbital from
-1
electron system is approximated by the Ansatz of eliminating an
orbital from ![]() :
:
The valence orbital to be eliminated, ![]() , will be
determined variationally. This Ansatz is reminiscent of a
quasiparticle wave function for the state, although the
formulation is for
, will be
determined variationally. This Ansatz is reminiscent of a
quasiparticle wave function for the state, although the
formulation is for ![]() -1 particle eigenstates of the Hamiltonian.
Expressing equation 7.9 in second quantization yields
-1 particle eigenstates of the Hamiltonian.
Expressing equation 7.9 in second quantization yields
| (7.10) |
The ionisation energy is given by the difference in the expectation
values of the Hamiltonian calculated with the ![]() and
and ![]() -1 electron
wave functions:[99,133]
-1 electron
wave functions:[99,133]
If ![]() is an eigenfunction of
is an eigenfunction of ![]() ,
equation 7.11 may be written as
,
equation 7.11 may be written as
The denominator in equation 7.12 is the one-body
density matrix. Solution of this equation is facilitated by expanding
in a set of orbitals, ![]() , so that
, so that
![]() , and
, and
![]() ,
where
,
where ![]() is the destruction operator for
is the destruction operator for ![]() . The
condition for a stationary value of
. The
condition for a stationary value of ![]() generates a secular
equation
generates a secular
equation
The matrix ![]() is the one-body density matrix, and
the elements of
is the one-body density matrix, and
the elements of ![]() are
are
| (7.14) |
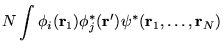 |
|||
| (7.15) |
![]() consists of the terms in the
consists of the terms in the ![]() -electron
Hamiltonian involving coordinate
-electron
Hamiltonian involving coordinate ![]() , so that
, so that
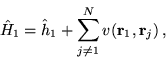 |
(7.16) |
where ![]() consists of the one-body kinetic energy
operator and ionic potential, including both local and non-local
pseudopotential components, and
consists of the one-body kinetic energy
operator and ionic potential, including both local and non-local
pseudopotential components, and ![]() is the electron-electron
interaction potential.
is the electron-electron
interaction potential.
If a HF wave function is used for ![]() and the density matrix is
expanded in a basis set of HF orbitals, then
and the density matrix is
expanded in a basis set of HF orbitals, then ![]() reduces to a
matrix with the HF
reduces to a
matrix with the HF ![]() -particle eigenvalues on the occupied part of
the diagonal, and zeros everywhere else. The resulting excitation
energies are those given by the well-known Koopmans'
theorem.[112] The contents of the EKT method are now
reasonably clear. The method consists of a quasiparticle-like Ansatz
for the wave function of the
-particle eigenvalues on the occupied part of
the diagonal, and zeros everywhere else. The resulting excitation
energies are those given by the well-known Koopmans'
theorem.[112] The contents of the EKT method are now
reasonably clear. The method consists of a quasiparticle-like Ansatz
for the wave function of the ![]() -1 particle system, which is used to
calculate the ionisation energies of the system. Electron
correlations are included, but no allowance is made for relaxation of
the other orbitals in the presence of the excitation. Although this
relaxation can be important in small systems, it is expected to
be much less important for excitations in extended systems such as the
silicon crystal studied here.
-1 particle system, which is used to
calculate the ionisation energies of the system. Electron
correlations are included, but no allowance is made for relaxation of
the other orbitals in the presence of the excitation. Although this
relaxation can be important in small systems, it is expected to
be much less important for excitations in extended systems such as the
silicon crystal studied here.
An analogous theory exists for the conduction band energies. The wave
function for the ![]() +1 electron system is approximated by the Ansatz
of adding an orbital to
+1 electron system is approximated by the Ansatz
of adding an orbital to ![]() :
:
where
![]() is the antisymmetriser and the
orbital
is the antisymmetriser and the
orbital ![]() is to be determined variationally. In second
quantization we have
is to be determined variationally. In second
quantization we have
| (7.18) |
The excitation energies ![]() are defined by
are defined by
Expanding in a set of orbitals gives
![]() and
and
![]() . The coefficients
. The coefficients ![]() are the solutions of the
secular equation
are the solutions of the
secular equation
where the matrix elements are
![]() and
and
![]() .
.
It is instructive to introduce a new potential with matrix elements
![]() :
:
If an HF wave function a basis of HF orbitals is used,
![]() reduces to a matrix with the HF
reduces to a matrix with the HF ![]() -particle eigenvalues on
the diagonal, and zeros everywhere else. In this case one can readily
identify the second and third terms in equation 7.21 as,
respectively, the Hartree and exchange terms. (Similarly
-particle eigenvalues on
the diagonal, and zeros everywhere else. In this case one can readily
identify the second and third terms in equation 7.21 as,
respectively, the Hartree and exchange terms. (Similarly ![]() reduces to the HF energy eigenvalues on the unoccupied part of the
diagonal.)
reduces to the HF energy eigenvalues on the unoccupied part of the
diagonal.)
The matrix elements of ![]() and
and ![]() were accumulated,
subsequently forming the matrix
were accumulated,
subsequently forming the matrix
![]() . The
matrix elements,
. The
matrix elements, ![]() , are given by
, are given by
As before, permutation symmetry allows this to be rewritten as
so that ![]() values are accumulated at each step. The terms
contributing to
values are accumulated at each step. The terms
contributing to
![]() are already available in a VMC
calculation, allowing
are already available in a VMC
calculation, allowing ![]() to be accumulated with virtually no
additional cost beyond that required for the density matrix. An
analogous VMC formulation for calculating
to be accumulated with virtually no
additional cost beyond that required for the density matrix. An
analogous VMC formulation for calculating ![]() exists. The single
particle terms,
exists. The single
particle terms, ![]() , appearing in the first term in
equation 7.21 were evaluated directly without use of Monte Carlo
integration. Using Monte Carlo integration for all the terms resulted
in a small increase in the variance of the matrix elements. It is
therefore preferable, but less elegant, to calculate the
, appearing in the first term in
equation 7.21 were evaluated directly without use of Monte Carlo
integration. Using Monte Carlo integration for all the terms resulted
in a small increase in the variance of the matrix elements. It is
therefore preferable, but less elegant, to calculate the ![]() terms directly. The matrix elements
terms directly. The matrix elements ![]() and
and ![]() were
accumulated at the same time as the elements
were
accumulated at the same time as the elements ![]() . The full
crystal symmetry was again used, which reduces the number of matrix
elements which must be accumulated and ensures the correct symmetry in
the presence of statistical noise.
. The full
crystal symmetry was again used, which reduces the number of matrix
elements which must be accumulated and ensures the correct symmetry in
the presence of statistical noise.
The correlation lengths along the VMC walks for ![]() and
and
![]() were found to be similar to those of the local energy and
density matrix, and the distribution of statistical errors was similar
to that for the density matrix. The elements of
were found to be similar to those of the local energy and
density matrix, and the distribution of statistical errors was similar
to that for the density matrix. The elements of ![]() and
and
![]() with the largest statistical errors were the diagonal
elements. The statistical error bars on these elements are estimated
to be
with the largest statistical errors were the diagonal
elements. The statistical error bars on these elements are estimated
to be ![]() eV.
eV.
The matrix equations 7.13 and 7.20 were
diagonalised using a generalized eigenvalue solver. The ratios of the
statistical error bars to the mean values were significantly larger
for the diagonal elements of ![]() and
and ![]() than for
than for
![]() . Just as for the density matrix, small perturbations were
applied to estimate the statistical errors in the eigenvalues and
eigenvectors. The numerical stability of the diagonalisation was
improved by explicitly zeroing elements of
. Just as for the density matrix, small perturbations were
applied to estimate the statistical errors in the eigenvalues and
eigenvectors. The numerical stability of the diagonalisation was
improved by explicitly zeroing elements of ![]() and
and ![]() within statistical error of zero. The accuracy of the eigenvalues was
further verified by gradually increasing the number of bands in the
diagonalisation procedure. The valence and low lying conduction band
energies were stable to within
within statistical error of zero. The accuracy of the eigenvalues was
further verified by gradually increasing the number of bands in the
diagonalisation procedure. The valence and low lying conduction band
energies were stable to within ![]() eV.
eV.
The resulting band energies are shown in figure 7.3
and given in table 7.2, with the energy at the top of
the valence band set to zero. Of the k-points computed here,
the available experimental data (Exp) is limited to the
![]() -point. Because of this we also give empirical
pseudopotential (Emp) data [135] in table
7.2 and in figure 7.3. The
empirical pseudopotential data should
provide a good interpolation between this data. Results for the Ewald
and MPC interactions are in good agreement, indicating that the
finite size errors are not significant at the level of statistical
accuracy obtained here. The energies are in good qualitative
agreement with the empirical data at all k-points except for the
upper
-point. Because of this we also give empirical
pseudopotential (Emp) data [135] in table
7.2 and in figure 7.3. The
empirical pseudopotential data should
provide a good interpolation between this data. Results for the Ewald
and MPC interactions are in good agreement, indicating that the
finite size errors are not significant at the level of statistical
accuracy obtained here. The energies are in good qualitative
agreement with the empirical data at all k-points except for the
upper ![]() valence band state, and the
valence band state, and the
![]() conduction band state. The source of the error is principally the
value of the diagonal matrix elements for these states,
conduction band state. The source of the error is principally the
value of the diagonal matrix elements for these states, ![]() and
and
![]() (see next section).
(see next section).
![\includegraphics [width=10cm]{Figures/ekt_fig3.eps}](pkthimg831.gif)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The EKT band energies at the ![]() -point are in good agreement with
the available experimental data, and are also in good agreement with
the DMC data from direct calculations of the excitation
energies.[103] The EKT valence band width of
-point are in good agreement with
the available experimental data, and are also in good agreement with
the DMC data from direct calculations of the excitation
energies.[103] The EKT valence band width of
![]() eV is smaller than the value of
eV is smaller than the value of ![]() eV obtained from
the DMC calculations and is in good agreement with the experimental
value of
eV obtained from
the DMC calculations and is in good agreement with the experimental
value of ![]() eV. In comparison the HF data shows the well known
overestimation of band gaps and band widths which is due to the
neglect of correlation energy, the LDA gives excellent valence band
energies while the conduction bands are too low in energy by 0.7-1.0
eV, and the
eV. In comparison the HF data shows the well known
overestimation of band gaps and band widths which is due to the
neglect of correlation energy, the LDA gives excellent valence band
energies while the conduction bands are too low in energy by 0.7-1.0
eV, and the ![]() data is in very good agreement with experiment.
data is in very good agreement with experiment.
The EKT is a formulation for the eigenstates of the ![]() -1 and
-1 and ![]() +1
electron systems, while the direct method is aimed at calculating the
eigenstates of the
+1
electron systems, while the direct method is aimed at calculating the
eigenstates of the ![]() electron system. The EKT and direct results
should therefore differ by the exciton binding energy, but this energy
is small for silicon and cannot be resolved at the level of
statistical accuracy obtained. Depending on the application one would
like to be able to choose whether to include excitonic effects, so
that it is advantageous to have the different QMC techniques
available. Clearly further refinement of excited state QMC methods is
required, but the results from the EKT and direct approaches are
promising for the study of more strongly correlated systems, for which
the LDA and
electron system. The EKT and direct results
should therefore differ by the exciton binding energy, but this energy
is small for silicon and cannot be resolved at the level of
statistical accuracy obtained. Depending on the application one would
like to be able to choose whether to include excitonic effects, so
that it is advantageous to have the different QMC techniques
available. Clearly further refinement of excited state QMC methods is
required, but the results from the EKT and direct approaches are
promising for the study of more strongly correlated systems, for which
the LDA and ![]() methods are less reliable.
methods are less reliable.
If the off-diagonal elements of ![]() ,
, ![]() , and
, and
![]() are neglected then the valence and conduction band
energies can be approximated by
are neglected then the valence and conduction band
energies can be approximated by
where the superscript DEKT denotes the diagonal approximation to the EKT. This approximation has been used within VMC and without reference to the EKT by Fahy et al. [121] to calculate quasihole energies in silicon and also by Tanaka[122] to calculate the quasihole energies in NiO. This approximation has the computational advantage that far fewer matrix elements are required, and also that the problems of statistical noise are reduced, because the values of only two matrix elements enter the calculation of each band energy. However the results are basis set dependent, and could differ significantly between, for example, a HF and LDA basis.
If an HF wave function and basis set of HF orbitals is used then the
matrices ![]() ,
, ![]() , and
, and ![]() are all diagonal, and
consequently the full EKT and the DEKT are equivalent. In general,
for correlated wave functions, the DEKT gives neither an upper nor
lower bound to the energy obtained from the full EKT. Comparison with
the data from the DEKT is made in table 7.2. The DEKT
values are close to the full EKT values, including the two cases
mentioned above where the agreement with experiment is poor. The DEKT
works quite well for the valence bands and slightly less well for the
conduction bands, because the off-diagonal matrix elements of
are all diagonal, and
consequently the full EKT and the DEKT are equivalent. In general,
for correlated wave functions, the DEKT gives neither an upper nor
lower bound to the energy obtained from the full EKT. Comparison with
the data from the DEKT is made in table 7.2. The DEKT
values are close to the full EKT values, including the two cases
mentioned above where the agreement with experiment is poor. The DEKT
works quite well for the valence bands and slightly less well for the
conduction bands, because the off-diagonal matrix elements of
![]() coupling the unoccupied states are more significant. In
similar VMC calculations for silicon using the DEKT and a smaller simulation
cell of 64 electrons, Fahy et al. [121]
calculated a valence band width of 14.5(4) eV, which is larger than
the value of 13.3(2) eV and the experimental value of 12.5(6) eV.
Fahy et al. [121] also obtained occupation numbers of
1.96(4) and 1.92(3) for the
coupling the unoccupied states are more significant. In
similar VMC calculations for silicon using the DEKT and a smaller simulation
cell of 64 electrons, Fahy et al. [121]
calculated a valence band width of 14.5(4) eV, which is larger than
the value of 13.3(2) eV and the experimental value of 12.5(6) eV.
Fahy et al. [121] also obtained occupation numbers of
1.96(4) and 1.92(3) for the ![]() and
and
![]() valence band states respectively, compared with the values of
1.9817(2) and 1.9375(5) obtained in the larger cell of this study.
valence band states respectively, compared with the values of
1.9817(2) and 1.9375(5) obtained in the larger cell of this study.
The scaling with system size of the diagonal approximation is very
advantageous compared with direct evaluation of excitation energies.
In direct methods, the fractional energy change due to the promotion
of an electron is considered. This energy change is inversely
proportional to the number of electrons in the system, i.e., a
`![]() ' effect. The precision of the calculation must
therefore be sufficient to resolve the energy change amid the
statistical noise. This requirement is very challenging for small band
gap materials, as the system must also be sufficiently large to
approximate the infinite solid. In the DEKT, the band energies are
computed directly as averages over the square of the ground state wave
function, rather than as the difference between averages over the
squares of the ground and excited state wave functions. This greatly
improves the sampling statistics. We have found that the errors in
' effect. The precision of the calculation must
therefore be sufficient to resolve the energy change amid the
statistical noise. This requirement is very challenging for small band
gap materials, as the system must also be sufficiently large to
approximate the infinite solid. In the DEKT, the band energies are
computed directly as averages over the square of the ground state wave
function, rather than as the difference between averages over the
squares of the ground and excited state wave functions. This greatly
improves the sampling statistics. We have found that the errors in
![]() ,
, ![]() and
and ![]() scale as the inverse of the
square root of the number of independent electron configurations,
independently of the system size. For sufficiently large systems, it
therefore requires fewer statistically independent samples in the DEKT
to obtain excitation energies to a given statistical accuracy than
with direct methods. The scaling behavior of the full EKT is more
difficult to analyze because we are required to diagonalise noisy
matrix equations, where the number of off-diagonal matrix elements
increases as the square of the system size, and where there are
certainly statistical correlations between matrix elements.
scale as the inverse of the
square root of the number of independent electron configurations,
independently of the system size. For sufficiently large systems, it
therefore requires fewer statistically independent samples in the DEKT
to obtain excitation energies to a given statistical accuracy than
with direct methods. The scaling behavior of the full EKT is more
difficult to analyze because we are required to diagonalise noisy
matrix equations, where the number of off-diagonal matrix elements
increases as the square of the system size, and where there are
certainly statistical correlations between matrix elements.