Two quantities are required during a QMC calculation: the ratio of the
old to new determinant when a single electron is moved, and the
updated determinant when a single electron move is accepted. Although
similar, the first of these operations is a ![]() process, the second
process, the second
![]() . There are
. There are ![]() accepted single electrons moves per
``configuration move'' giving rise to the
accepted single electrons moves per
``configuration move'' giving rise to the ![]() scaling of QMC
methods.
scaling of QMC
methods.
It has been shown [50,26,23] that it is possible to work entirely with the matrix of cofactors of the Slater determinant. This also applies to multi-determinant wavefunctions.
The Slater determinant has elements
| (4.15) |
The relation
| (4.17) |
| (4.18) |
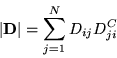 |
(4.19) |
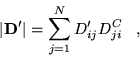 |
(4.20) |
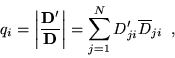 |
(4.21) |
If the move of electron ![]() to position
to position
![]() is accepted,
the matrix of cofactors is updated:
is accepted,
the matrix of cofactors is updated:
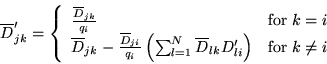 |
(4.22) |
| (4.23) |
| (4.24) |
Calculation of the potential energies requires evaluation of the election-ion and electron-electron potentials. For pseudopotential calculations, the electron-ion potential is evaluated using the technique of section 4.5.1. The remaining Coulomb potentials are evaluated by direct summation in finite systems, and by Ewald summation (see section 4.6.1) in periodic systems.
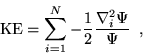 |
(4.25) |
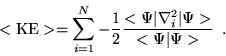 |
(4.26) |
The kinetic energy contribution from a single electron,
![]() , is most conveniently evaluated by defining two
additional quantities,
, is most conveniently evaluated by defining two
additional quantities, ![]() and
and ![]() :
:
Then the kinetic energy is given by
The use of logarithms is particularly convenient for Slater-Jastrow
wavefunctions (section 4.3.1). For a single-determinant
wavefunction, written as a product of spin up and down determinants,
| (4.30) |
| (4.31) |
Averaging the quantities ![]() and
and ![]() independently
provides a useful check on the simulation. In VMC, Green's relation shows that
independently
provides a useful check on the simulation. In VMC, Green's relation shows that
| (4.32) |
The Ewald sum consists of separate real and reciprocal space sums. For computational efficiency, an optimised Ewald sum is used in which only a single real space term is taken. The sum is therefore biased towards the reciprocal space part which is more rapidly evaluated. An optimised form for the real and reciprocal space potentials [52] minimises errors.
To parallelise the VMC algorithm it is sufficient to note that
provided care is taken to ensure each calculation uses a different
random number sequence, the algorithm can be parallelised by performing
independent VMC calculations on each node of a parallel
machine. Communication between the nodes is only necessary to obtain
global averages and is therefore negligible: the parallel efficiency
is essentially ![]() , and the calculation can theoretically exploit any
number of nodes without loss of efficiency.
, and the calculation can theoretically exploit any
number of nodes without loss of efficiency.
During a DMC calculation an ensemble of walkers is propagated in imaginary time. It is natural to divide the walkers evenly amongst the nodes, so that communication is only strictly necessary at the end of each block, when the population is renormalised. However, this simple modification would result in a low parallel efficiency because the calculation would become poorly load balanced as the calculation progressed. The branching and deletion of walkers would result in some nodes having more walkers than others; at the end of the block many nodes would have to wait whilst others moved their remaining walkers. A load balanced DMC algorithm requires the even distribution of walkers over all nodes, and this is accomplished by redistributing the walkers after every move.
Therefore, in the parallel DMC algorithm, walkers are initially evenly distributed over all nodes. Each node is then responsible for propagating its walkers. After each ``ensemble move'', the walkers are redistributed as evenly as possible across all of the nodes.
The parallel efficiency is limited by two factors:
In general, the walkers are not evenly distributed between nodes and
the first limitation results from the time lost while nodes complete
moving all of their walkers. The efficiency of the algorithm is given
by
| (4.33) |
The accuracy of the guiding wavefunction governs the fluctuations in
the walker population. Hence improved guiding wavefunctions have the
combined effect of increasing the statistical accuracy of the
calculations and increasing the efficiency with which they are carried
out. For the calculations in this thesis, parallel efficiencies of
![]() were typical.
were typical.