![\includegraphics [width=10cm]{Figures/supercell.eps}](pkthimg423.gif)
|
The supercell method is the ubiquitous approach for the study of solid-state periodic boundary condition systems. In principle, a solid may also be approximated by means of a large cluster. For sufficiently large clusters, the quantum mechanics of the centre-most atoms approximate those in a solid. However, the size of cluster required to approximate a solid is large due to the dominance of surface over ``bulk'' atoms in small and medium sized clusters. This consideration applies to all electronic structure methods, and the best general solution is to use a limited number of repeats of a primitive cell combined with periodic boundary conditions, as illustrated in figure 4.2.
![\includegraphics [width=10cm]{Figures/supercell.eps}](pkthimg423.gif)
|
In the supercell approach, [73,17] an artificial periodicity is imposed on the simulation cell to better model the continuum properties of the system. Bloch's theorem may then be applied to the wavefunctions.
For perfect crystals, a limited number of repeats of the primitive cell are used. Periodic boundary conditions impose an artificial periodicity on interactions in the system. The supercell must be large enough that these spurious interactions are small. These finite size effects are examined in detail in chapter 6.
Ewald's method [51,74,75,17] is a near exact method for the evaluation of long-ranged interactions within periodic boundary conditions. The interaction terms forming the potential are rearranged into two series that are readily evaluated.
To illustrate the method, we consider a cubic supercell containing ![]() particles of charge
particles of charge ![]() . The interaction energy can be written as
. The interaction energy can be written as
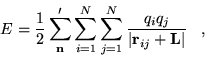 |
(4.40) |
In the Ewald method, the point charge distribution is modified to give
two convergent series, the sum of which gives the correct value
for the unmodified distribution. The neutral Ewald ``charge density''
is given by a sum over the point charges plus a screening background.
| (4.41) |
The Ewald potential is computed as a sum of two components. An array
of Gaussians are used in both: in the first, the Gaussians cancel the
background charge density, and in the second, the Gaussians are
subtracted from the delta function charge distribution (see
figure 4.3). The width of the Gaussian charges, ![]() ,
controls the rate of convergence of the two series and is usually
optimised for each supercell.
,
controls the rate of convergence of the two series and is usually
optimised for each supercell.
![\includegraphics [width=10cm]{Figures/ewald.eps}](pkthimg434.gif)
|
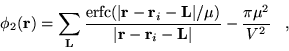 |
(4.44) |
| (4.45) |
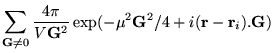 |
|||
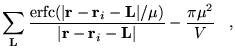 |
(4.46) |
This potential could be used to compute the electron-ion
potential. The Ewald sum for the electron-electron potential is
similar, but the ``self-image'' of an electron is removed, due to the
periodic array of images and Gaussian charges. Electrostatic energies
are computed by multiplying the Ewald potential by the appropriate
product of charges ![]() .
In terms of speed and accuracy, for small numbers of particles (1000
or less), a well implemented version of Ewald's method has yet to be
improved on. The computational cost Ewald's method, for a specified
accuracy, scales as
.
In terms of speed and accuracy, for small numbers of particles (1000
or less), a well implemented version of Ewald's method has yet to be
improved on. The computational cost Ewald's method, for a specified
accuracy, scales as ![]() . [77] Large numbers of
particles are more efficiently dealt with using multipole expansions,
based on hierarchical spatial subdivision of the charge
density. [78,79] The largest supercell
calculation in this thesis involves 1000 electrons (see
chapter 6), and Ewald's method was applied in this case.
. [77] Large numbers of
particles are more efficiently dealt with using multipole expansions,
based on hierarchical spatial subdivision of the charge
density. [78,79] The largest supercell
calculation in this thesis involves 1000 electrons (see
chapter 6), and Ewald's method was applied in this case.