


Next: 4.9 Summary
Up: 4. Implementation
Previous: 4.7 Wavefunction optimisation
Contents
Subsections
The efficient generation and accurate analysis of data is central to
all Monte Carlo simulations. In this section the statistical techniques
used to compute the expected value of observables and then error bars are
described. The techniques are similar to those used in other Monte
Carlo and molecular dynamics methods, and the observables, though
normally energies, can in principle be any quantity.
When analysing the data, two factors that must be taken into account
are the equilibration (or relaxation) time of the observable, and the
likely presence of serial correlations in the data. Compensating for
correlations is essential in order to obtain an accurate error bar.
For the purposes of this section, a set of  sequentially observed
data values
sequentially observed
data values 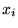 will be considered. The values of
will be considered. The values of 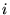 correspond
to simulation times
correspond
to simulation times 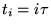 , where
, where 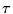 is the Monte Carlo
timestep between samples.
is the Monte Carlo
timestep between samples.
The mean or average value of the observable is given straightforwardly,
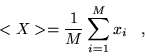 |
(4.49) |
however evaluation of the error bar (the standard deviation of the mean)
is more involved due to the likelyhood of serial correlations. The
correlation time, 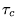 is a measure of how long it takes the
system to evolve between states that are independent. The
correlation time is conventionally defined [16]
via the autocorrelation function of the data,
is a measure of how long it takes the
system to evolve between states that are independent. The
correlation time is conventionally defined [16]
via the autocorrelation function of the data, 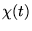 ,
,
![\begin{displaymath}
\chi(t)=\int [x(t^\prime)x(t^\prime+t)-<x>^2]dt^\prime
\end{displaymath}](pkthimg466.gif) |
(4.50) |
The autocorrelation function is
defined such that 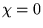 for completely uncorrelated data and
for completely uncorrelated data and
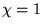 for completely correlated data. At long times, Markovian
processes are expected to lead to an exponentially decay in
for completely correlated data. At long times, Markovian
processes are expected to lead to an exponentially decay in 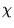 ,
,
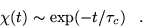 |
(4.51) |
The autocorrelation function, equation 4.50, is estimated
by [16]
Assuming the central limit theorem holds and following the conventional
statistical definitions, [19]
the best estimate of the
standard deviation of the mean is given by
![\begin{displaymath}
\sigma=\sqrt{\frac{2\tau_c}{M\tau}\left[\frac{1}{M}\sum_{i=1...
..._{i}^{2}-(\frac{1}{M}\sum_{i=1}^{M} x_{i})^{2}\right]} \;\;\;.
\end{displaymath}](pkthimg473.gif) |
(4.53) |
A simpler approach based on a reblocking of the data can be used in
practice. In the reblocking scheme data is grouped into a series of
block sizes, 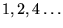 , and the standard deviation obtained by
computing the variance of the block averages. For each block size, an
estimate of the standard deviation of the mean can be shown to
be [16,75]
, and the standard deviation obtained by
computing the variance of the block averages. For each block size, an
estimate of the standard deviation of the mean can be shown to
be [16,75]
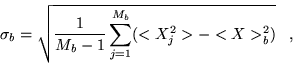 |
(4.54) |
where 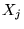 is an average over block
is an average over block 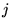 ,
, 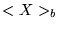 the average over
all blocks and
the average over
all blocks and 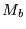 is the number of blocks. The standard deviation
of the mean is proportional to the square root of the mean squared
deviation in block averages, assuming a sufficient number of blocks
and samples are included in the analysis.
is the number of blocks. The standard deviation
of the mean is proportional to the square root of the mean squared
deviation in block averages, assuming a sufficient number of blocks
and samples are included in the analysis. 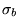 increases with
block length
increases with
block length 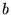 until a limiting value is reached, and this value
corresponds to the true standard deviation of the mean. Where is an
insufficient volume of data,
a limiting value of
until a limiting value is reached, and this value
corresponds to the true standard deviation of the mean. Where is an
insufficient volume of data,
a limiting value of 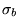 is not reached. Other methods for
computing the standard deviation of the mean, such as the jackknife and
bootstrap procedures, [16] give similar
results. An example of the reblocking analysis is shown in figure
4.4.
is not reached. Other methods for
computing the standard deviation of the mean, such as the jackknife and
bootstrap procedures, [16] give similar
results. An example of the reblocking analysis is shown in figure
4.4.
Figure 4.4:
Reblocking of DMC energies. For
this data, the reblocked error bar is the limiting value of
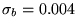 eV. When insufficient data is reblocked,
eV. When insufficient data is reblocked,
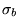 (equation 4.54)
does not reach a limiting value with increasing block length.
(equation 4.54)
does not reach a limiting value with increasing block length.
|
|
In VMC calculations an accurate estimate of the correlation length can
be used to improve the efficiency of the simulation. In VMC
calculations an energy measurement is costly compared with a
Metropolis move. It is therefore efficient to only measure energies
at timesteps approximately equal to the correlation time. The
correlation time is system and wavefunction dependent but may be
accurately determined using only short Monte Carlo runs. This
criterion is also applicable when configurations are generated for
wavefunction optimisation (see section 4.7).
The equilibration time of an observable in a VMC calculation is best
determined by graphing the observable as a function of
time. Equivalently, trends block averages may be used where the data is divided
into short blocks. After equilibrating, the observable
fluctuates around its final mean value. A further check, used in all
calculations in this thesis, is to divide the complete set of data
into halves or thirds. For a sufficiently long simulation, the
averages of each block should agree to within error bars.
In DMC calculations an accurate estimate of the correlation length is
essential as the calculations are typically one order of magnitude
more expensive than VMC, partly due to the increased correlation
length observed in DMC calculations. The increased correlation length
results from the shorter timestep used in DMC calculations which are
necessary to limit the errors in the short time approximation to the
Green's function.
The ensemble average energy is computable at every timestep in DMC, as
the individual walker energies are required to compute the branching
factors. Equilibration is best judged by examining a graph of the
ensemble average energy and DMC walker population against time. For
observables other than the energy, it is not necessary to measure the
observable at every step and the techniques used in VMC are
applicable. Reblocking of the DMC data after equilibration gives
accurate error bars.
In addition to the checks described for VMC calculations, comparing
running averages with the overall average is a further useful method
to check that there are no long term trends in the data. A long term
downward trend in energy can result from a poor guiding wavefunction,
which effectively increases the equilibration and correlation times
for the system. The DMC walker population provides a further guide:
the population is stable when the reference energy is equal to the
fixed-node ground state energy. Figure 4.5 shows an
example DMC calculation.
Figure 4.5:
An example DMC calculation: Energies versus
move number and (inset) walker population versus move number. During
the initial equilibration stage, approximately 300 ensemble moves, the
ensemble average energy rapidly decays to the fixed-node ground state
energy and the trial energy, 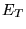 , is updated frequently to maintain
the population of the ensemble close to a target value. After the
excited states have propagated out the trial energy is only updated
occasionally to avoid population control errors. For this data, the
DMC energy would be computed after discarding approximately the first
1000 moves. (Inset) During equilibration, the walker population
increases rapidly and must be renormalised. After
equilibration, the walker population remains stable around the target
value of 640.
, is updated frequently to maintain
the population of the ensemble close to a target value. After the
excited states have propagated out the trial energy is only updated
occasionally to avoid population control errors. For this data, the
DMC energy would be computed after discarding approximately the first
1000 moves. (Inset) During equilibration, the walker population
increases rapidly and must be renormalised. After
equilibration, the walker population remains stable around the target
value of 640.
|
|
In the previous two sections, statistical techniques for the analysis
of QMC data were presented. These techniques are unable to detect any
systematic errors which could be present in the simulation.
Potential systematic errors include:
- Insufficient exploration of configuration space results if a
simulation is run for too short a period of time, or if the timestep
chosen severely limits the number of accepted Monte Carlo moves. (The
ratio of accepted to proposed moves is typically
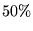 in VMC and
in VMC and
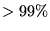 in DMC calculations.)
in DMC calculations.)
- Inclusion of unequilibrated data in final averaged data gives a
systematic bias to the averages obtained.
- Updating the trial energy or renormalising the
number of walkers in the ensemble too frequently results in population
control errors, and the true ground state distribution and energy
is not obtained.
- In DMC calculations, a systematic timestep error will always be
present due to the approximation used for the Green's function. For
every system, DMC calculations must be repeated with progressively
smaller timesteps until results agree to within error bars at the
final level of statistical accuracy desired.
Systematic errors can be avoided by careful benchmarking of new
systems. When doing so it is important to consider possible changes in
wavefunction quality as system size and geometry is changed. The
cancellation of remaining timestep and other systematic errors in
energy differences may be encouraged by choosing a fixed timestep and
block size (period between population renormalisation) for all
calculations. However, the calculations should always be setup such
that these errors are not significant even if no cancellation takes
place.



Next: 4.9 Summary
Up: 4. Implementation
Previous: 4.7 Wavefunction optimisation
Contents
© Paul Kent
![]() sequentially observed
data values
sequentially observed
data values ![]() will be considered. The values of
will be considered. The values of ![]() correspond
to simulation times
correspond
to simulation times ![]() , where
, where ![]() is the Monte Carlo
timestep between samples.
is the Monte Carlo
timestep between samples.
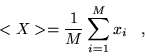
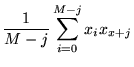
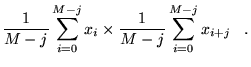
![\begin{displaymath}
\sigma=\sqrt{\frac{2\tau_c}{M\tau}\left[\frac{1}{M}\sum_{i=1...
..._{i}^{2}-(\frac{1}{M}\sum_{i=1}^{M} x_{i})^{2}\right]} \;\;\;.
\end{displaymath}](pkthimg473.gif)
![]() , and the standard deviation obtained by
computing the variance of the block averages. For each block size, an
estimate of the standard deviation of the mean can be shown to
be [16,75]
, and the standard deviation obtained by
computing the variance of the block averages. For each block size, an
estimate of the standard deviation of the mean can be shown to
be [16,75]
![\includegraphics [width=12cm]{Figures/reblocking.eps}](pkthimg481.gif)
![\includegraphics [width=12cm]{Figures/dmchist.eps}](pkthimg483.gif)