7.3 The density matrix and natural orbitals

The one-body density matrix, defined in equation 7.1, is conventionally expanded in a basis of orbitals, $\phi_i$, where

$$\rho({\bf r},{\bf r}^\prime) = \sum_{i,j} \rho_{ij}\phi_i({\bf r})\phi^*_j({\bf r}^\prime)\,.$$ (7.2)

The diagonal elements, $\rho_{ii}$, are commonly referred to as the orbital occupation numbers. For wave functions consisting of a single determinant, such as HF or LDA wave functions, the density matrix is idempotent $(\rho=\rho^2)$ and takes the form of a sum over the occupied orbitals, i.e.,

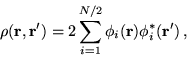$$\rho({\bf r},{\bf r}^\prime) = 2 \sum_{i=1}^{N/2} \phi_i({\bf r})\phi^*_i({\bf r}^\prime)\,,$$ (7.3)

so that the occupation numbers are 2 (including spin degeneracy) for occupied orbitals and 0 for unoccupied orbitals.

The matrix elements of the interacting density matrix, $\rho_{ij}$, are written as expectation values over the distribution $\left\vert \psi \right\vert ^2$:

$$\rho_{ij}=N\int \phi^*_i({\bf r}_1)\phi_j({\bf r}^\prime) \frac{\... ...f r}^\prime,{\bf r}_2,\ldots,{\bf r}_{N})}{\psi( {\bf r}_1,\ldots,{\bf r}_{N})}$$

$$\times \left\vert \psi( {\bf r}_1,\ldots,{\bf r}_{N})\right\vert ^2 d{\bf r}^\prime d{\bf r}_1\ldots d{\bf r}_N\,.$$ (7.4)

The permutation symmetry allows a rewriting of equation 7.4 in an efficient way for Monte Carlo evaluation. Denoting the average over the distribution, $\left\vert \psi \right\vert ^2$, as $\left<\ldots\right>_{\vert\psi\vert^2}$, the Monte Carlo expectation value is rewritten as

$$\rho_{ij}= \left<\,\sum_{n=1}^N \int \phi^*_i({\bf r}_n)\phi_j({\... ...s)}{\psi( \ldots,{\bf r}_n,\ldots)} d{\bf r}^\prime \right>_{\vert\psi\vert^2},$$ (7.5)

so that $N$ values are accumulated at each step along the VMC walk.

The integral over $d{\bf r}^\prime$ is performed by summing over a grid of uniform spacing whose origin is chosen randomly for each electron configuration. The same grid in ${\bf r}^\prime$ is used for each term in equation 7.5, which further reduces the computational cost. A series of grid sizes were tested for the ${\bf r}^\prime$ integral, using identical configurations for each grid size to obtain a correlated sampling estimate[23] of the difference between the integrals. A grid containing 125 points in the simulation cell was tested and found to sample the integral with sufficient numerical accuracy.

Provided that the density of points in the ${\bf r}^\prime$ integral is kept constant, the statistical error in the individual elements of the density matrix for a given number of statistically independent configurations is approximately independent of system size.

A basis set consisting of the lowest energy LDA orbitals at the 27 k-points in the primitive Brillouin zone was used. LDA orbitals were expected to form an efficient basis for the density matrix as the quasiparticle orbitals of silicon are very close to the LDA orbitals. The effect of varying the number of orbitals in the basis was tested, and approximately 40 orbitals per k-point were sufficient, although to retain the symmetry all rows of a degenerate representation (a degeneracy) were included, so that the actual number used was either 39 or 40 orbitals, depending on the k-point.

The normalization used in equation 7.1 requires that

$$N ={\rm T\!r}\rho \;,$$ (7.6)

which provides a practical test for the completeness of the basis set. The total occupation of the matrix (Tr$\rho$) was 215.9(2), which is within the statistical error of the number of electrons in the system, indicating sufficient completeness of the basis at the level for the statistical accuracy obtained.

7.3.1 Symmetry and efficiency considerations

Although for a given number of Monte Carlo moves, the best statistics were found to be obtained by accumulating all non-zero matrix elements and applying the symmetry afterwards, it was found to be computationally very expensive to accumulate all of them. A computationally more efficient procedure was found to involve accumulating only the independent non-zero matrix elements, and applying symmetry relationships to obtain the remaining elements. The basis set of LDA orbitals are basis functions of the unitary irreducible representations of the symmetry group $O_h^7$. Using the ``orthogonality condition for matrix representations''[123] it was inferred that elements involving products of orbitals from inequivalent k-points and of differing representations are zero. An explicitly fully symmetrised basis set was constructed numerically from a partially symmetrised basis set using the projection operator technique[123]. This procedure ensured that every occurrence of a given representation was identical, so that products between functions belonging to different rows were orthogonal. This procedure reduced the total number of independent and non-zero matrix elements, $\rho_{ij}$, from 42094 to 582 elements. This reduction resulted in substantial gains in computational efficiency, enabling substantially more accurate statistics to be obtained using the available computer time.

The 582 matrix elements were sampled using approximately 6.6$\times 10^5$ statistically independent configurations. The correlation lengths along the VMC walks of both the local energy and density matrix were found to be essentially the same.

7.3.2 Density matrix results

Elements of the accumulated density matrix, $\rho_{ii}$, are shown in figure 7.1. The accumulated density matrix, $\rho_{ij}$, was very nearly diagonal with little coupling between LDA orbitals. The occupation numbers decrease almost linearly with increasing LDA energy for both the occupied and unoccupied bands.

Denoting double occupancy (spin-up and down) of orbitals by the value $2.0$, the maximum difference between an interacting occupation number, $\rho_{ii}$, and the LDA occupation number was $0.0625(5)$. This difference occurred at the $\Gamma_{25'}$ state at the top of the valence band. The magnitude of the largest off-diagonal matrix element was $0.014(1)$, which is of similar order to the occupation number of the lowest unoccupied orbitals. The fractional errors in occupation numbers for orbitals of low occupation were large in comparison to those of high occupation. Approximately $97.6\%$ of the total occupation of the density matrix is contained within the four occupied LDA bands at each k-point, and $99.0\%$ is obtained within the first ten bands.

Figure 7.1: Occupation numbers (diagonal elements of the density matrix in the basis of LDA orbitals) plotted against the LDA energy for each k-point. These are the $\Gamma$-point($\circ$), $\Delta$ ($\Diamond$), $\Sigma$ ( $\bigtriangledown$), and $\Lambda$ ($\Box$), points on the $\Delta$, $\Sigma$, and $\Lambda$ axes respectively. The statistical error bars are approximately equal to the sizes of the symbols for the conduction band states and are about 5 times smaller than the symbols for the valence band states.

In figure 7.2 the density matrix, $\rho({\bf r},{\bf r}^\prime)$, in the (110) plane. The coordinate ${\bf r}$ is fixed at the center of a covalent bond, and ${\bf r}^\prime$ ranges over the (110) plane passing through the atomic positions. The small differences between the VMC and LDA matrices are shown separately. The density matrix consists of an asymmetric central peak, reduced in width along the bonding direction. A longer ranged structure is present in areas of high valence charge density, smaller by approximately one order of magnitude than the peak.

Figure 7.2: (a) The VMC one-body density matrix, $\rho_{\rm VMC}({\bf r},{\bf r}^\prime)$ and (b) $\rho_{\rm VMC}({\bf r},{\bf r}^\prime)-\rho_{\rm LDA}({\bf r},{\bf r}^\prime)$, in the (110) plane passing through the atoms with ${\bf r}$ fixed at the bond center. $\rho$ is normalized such that $\rho({\bf r},{\bf r})=n({\bf r})$, the charge density at the bond center. The silicon atoms and bonds are shown schematically.

The VMC value for the peak in the density matrix on the bond center at ${\bf r} \! = \! {\bf r}^\prime$ is $1.7\%$ smaller than the LDA value. The VMC density matrix has a larger magnitude around the neighboring silicon ions than the LDA density matrix, which consequently has a slightly smaller range. The density matrix was examined in the interstitial regions, where more structure was found. Again, the LDA and VMC results were very similar, with small differences between the two cases arising principally from the differing charge densities.

To investigate the possible finite size effects the LDA density matrices were computed for 3$\times$3$\times$3 and 4$\times$4$\times$4 k-point meshes, corresponding to simulation cells containing 54 and 128 atoms respectively. The central peak was largely unchanged and the longer ranged structure was in qualitative agreement. The central maximum in the density matrix, in figure 7.2, is at the point ${\bf r} \! = \! {\bf r}^\prime$ and its magnitude is directly proportional to the valence charge density at that point, which differed by $4.9\%$ between the two simulation cell sizes. These differences are small and indicate that no significant deviations between the LDA and VMC results are likely to be resolved by using a larger cell.

In exact Kohn-Sham density functional theory the total energy can be written entirely in terms of the one-body density matrix of the Kohn-Sham orbitals, whereas in a fully interacting system both the one-body density matrix and the pair-correlation function are required. Results for the pair-correlation function from accurate correlated wave functions and LDA calculations are extremely different.[14] Exact Kohn-Sham density functional theory reproduces the exact charge density and therefore exactly reproduces the diagonal ${\bf r}={\bf r}^{\prime}$ part of the density matrix. The off-diagonal part of the exact Kohn-Sham and interacting density matrices are not required to be the same. In silicon the LDA is expected to give a good approximation to the exact Kohn-Sham density matrix, as the LDA performs very well. For this system the results show that the entire density matrix is very similar in VMC and LDA. It is reasonable to speculate that the exact Kohn-Sham and exact one-body density matrices are probably very similar in other covalent sp systems.

7.3.3 Natural orbital results

The natural orbitals were obtained by diagonalising the density matrix in the basis of the LDA orbitals. An assessment of the statistical errors in the eigenvalues and eigenvectors was made by subjecting the matrix to random perturbations of order the statistical error. The eigenvalues varied by up to $\pm 0.0004$ on application of the small perturbations. All the calculated eigenvalues, $\lambda_i$, of the density matrix lie in the range $0 \! \le \! \lambda_i \! \le \! 2$, as is required.[109,110,111] Identical results were obtained when elements within statistical error of zero were explicitly zeroed. The overlap of the space occupied by the LDA orbitals and the natural orbitals is measured by the absolute value of the determinant of the matrix of overlaps between these two sets of vectors. This gave a value of 0.9948, indicating that the spaces spanned are almost the same.

The eigenvalues of the density matrix for the ``occupied'' natural orbitals were very slightly larger than the corresponding matrix elements $\rho_{ii}$ (by about $0.001$). Consequently, the eigenvalues of the ``unoccupied'' natural orbitals were very slightly decreased, so that ${\rm T\!r} \rho$ is invariant. Therefore a plot of the eigenvalues of the density matrix would be indistinguishable from figure 7.1, which shows the diagonal elements of the density matrix in the basis of LDA orbitals.

7.3.4 Relation to Compton profiles

Compton scattering is a form of inelastic x-ray scattering characterised by large energy and momentum transfer, and can be used to probe the electronic structure of materials by measuring the electron momentum distribution and its anisotropies. [124] Improvements in synchrotron x-ray sources have led to significant developments of this technique and resolutions of down to $\sim 0.02$ a.u. (at best) for momenta are currently possible. In this section, the zero momentum component of the momentum density for bulk silicon is determined from the density matrix and compared with previous results for the momentum density and Compton profile.

Accurate predictions of Compton profiles are desired to help confirm the more detailed information about electronic structure that simulations can provide; from accurate electronic structure calculations it should be possible to compute the experimentally observed Compton profile. At the time of writing, most theoretical calculations of Compton profiles have been computed using a single-particle framework such as LDA-DFT within the ``impulse approximation''. [125] Within this approximation, x-rays are considered to transfer momentum and energy to free electrons. [125] The Compton profile, $J({\bf q})$, is then given in terms of an integral of the momentum density, $N({\bf k})$,

$$J({\bf q})=\int N({\bf k}^\prime) \delta({\bf\hat q}.{\bf k}^{\prime}-q) d{\bf k}^\prime \;\;,$$ (7.7)

where the ${\bf k}^\prime$ integral is over the Brillouin zone. The momentum density, for a many-body system, is given by an expression similar to the expression for the density matrix (equation 7.1),

$$N({\bf k}) = \int \psi^*( {\bf r}_1,\ldots,{\bf r}_{N})\exp(i{\bf k}.{\bf s})$$

$$\times \psi( {\bf r}_1+{\bf s},{\bf r}_2,\ldots,{\bf r}_{N}) d{\bf s}d{\bf r}_1 \ldots d{\bf r}_N\;.$$ (7.8)

Recently, Králik et al. [126] and Filippi and Ceperley [127] computed the Compton profiles of bulk silicon and lithium respectively, using QMC techniques. Large deviations between experiment and the QMC results were apparent at small ${\bf q}$, although the results did improve on those of LDA-DFT calculations and were in agreement the Lam-Platzman correction [128] to the LDA-DFT results. This correction is in principle exact within DFT, but must be approximated using an approximate functional such as the LDA. The QMC calculations for bulk silicon [126] used a small simulation cell of 16 atoms. Hence, it is possible that finite-size effects and not the impulse approximation could be responsible for the residual discrepancy between the QMC results and experiment.

The value of $N(0)$ is given by equation 7.8 in terms of the natural orbitals of the density matrix and their occupancies. $N(0)$ was evaluated using the VMC density matrix for the 54 atom system used in this chapter. The results are shown in table 7.1 in terms of the difference between the VMC and LDA-DFT values.

Table 7.1: Calculated ${\bf k}=0$ components of the momentum density of bulk silicon, given as the difference between the VMC and LDA-DFT values. For this work, a 54 atom supercell was used, compared with the 16 atom supercell of Králik et al. [126]. (The units are the same as figure 1 of [126].)

$N_{\mathrm{VMC}}(0)-N_{\mathrm{LDA}}(0)$	Value (electrons/primitive cell)/(a.u.)$^3$
This work	-0.058(2)
Králik et al.	-0.053(10)

Although a larger supercell is used in this work, the value of $N(0)$ obtained is in good agreement with Králik et al. and has a smaller statistical error. This result strongly suggests that the finite size effects in the calculations are small, and that a similar Compton profile would be obtained if a full calculation was performed for the larger cell. In a later paper on the Compton profile of silicon,[129] Delaney et al. report that the effect of using pseudopotentials on the Compton profile is also small.

Filippi et al. [127] performed DMC calculations as well as VMC calculations for lithium. They found only very small differences in the momentum distribution between the two calculations indicating the VMC wavefunctions are of sufficient quality for this work. They also found deviations between experiment and the QMC results at small ${\bf q}$.

These results strongly support the conclusion that the residual difference between experiment and theory is not due to the treatment of electron-electron correlation in these materials. The residual differences in both silicon and lithium are therefore most likely due to a breakdown of the impulse approximation [125], although there may also be contributions from finite temperature effects that are not accounted in the experimental analysis.